Schwingungsvorgang in der Elektrotechnik und Elektronik, Schwingungsarten
Oszillatorischer Prozess – ein Prozess mit unterschiedlichem Grad an Wiederholbarkeit. Alle oszillierenden Prozesse werden in zwei Klassen eingeteilt: periodisch und nichtperiodisch. Theoretisch nutzen sie auch eine Zwischenklasse – nahezu periodische Schwingungen.
Als periodisch wird ein oszillierender Prozess bezeichnet, bei dem der diesen Prozess charakterisierende Wert zu jedem Zeitpunkt nach einer bestimmten Zeitspanne T den gleichen Wert hat.
Die Funktion f (t), die ein mathematischer Ausdruck des Schwingungsvorgangs ist, heißt periodisch mit der Periode T, wenn sie die Bedingung f (t + T) = f (t) erfüllt.
In der Klasse der periodischen Schwingungsprozesse spielen harmonische oder sinusförmige Schwingungen die Hauptrolle, bei denen eine zeitliche Änderung einer physikalischen Größe nach dem Sinus- oder Kosinusgesetz erfolgt. Ihre Gesamtbilanz lautet:
y = f (t) = aCos ((2π / T) t — φ),
Dabei ist a die Amplitude der Schwingungen, φ die Schwingungsphase, 1 /T = f die Frequenz und 2πf = ω die Frequenz der zyklischen oder kreisförmigen Schwingungen.
Anwendung von Sinusschwingungen und ihre Eigenschaften:
Grafische Möglichkeiten zur Darstellung von Wechselstrom
Eine nahezu periodische Funktion, die einer Ablesung periodischer Schwingungen entspricht, wird durch die Bedingung definiert:
| f · (t + τ) — f (t) | <= ε wobei ε – jedem Wert T einen Wert zuweisen.
Die Größe τ heißt in diesem Fall Fastperiode. Wenn der Wert ε im Vergleich zum Durchschnittswert von f (t) zum Zeitpunkt T sehr klein ist, liegt die quasiperiodische Funktion nahe an der periodischen.
Nichtperiodische Schwingungen sind viel vielfältiger als periodische. Am häufigsten kommt es jedoch in der Automatisierung zu Dämpfung oder zunehmenden Sinusschwingungen.
Schwingungen nach dem Gesetz der gedämpften Sinuskurve oder, wie sie manchmal genannt werden, gedämpfte harmonische Schwingungen, können in einer allgemeinen Form dargestellt werden:
x = Ae-δTcos·(ω + φ),
wobei t die Zeit ist, A und φ beliebige Konstanten sind. Die allgemeine Schreibweise des Gesetzes zunehmender harmonischer Schwingungen unterscheidet sich lediglich im Vorzeichen des Dämpfungsfaktors δ[1 Sekunde].
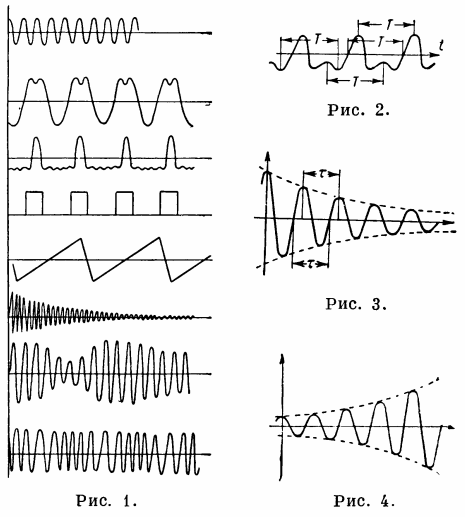
Feige. 1 – oszillierender Prozess, Abb. 2. – periodischer Prozess, Abb. 3. – abklingende harmonische Schwingungen, Abb. 4. — Zunahme harmonischer Schwingungen.
Ein Beispiel für die Anwendung des Schwingprozesses ist der einfachste Schwingkreis.
Oszillatorschaltung (Stromkreis) – ein passiver Stromkreis, in dem elektrische Schwingungen mit einer Frequenz auftreten können, die durch die Parameter des Stromkreises selbst bestimmt wird.
Der einfachste Schwingkreis besteht aus der Kapazität C und der Induktivität L. Ohne äußere Einwirkung dämpfen Schwingungen mit der Frequenz εО = 1/2π√LC.
Die Amplitude der Schwingungen nimmt mit zB-δT ab, wobei δ der Dämpfungskoeffizient ist. Wenn δ> = eO, dann werden die gedämpften Schwingungen im Stromkreis nichtperiodisch.
In der Elektronik wird die Güte des Schwingkreises durch den Gütefaktor bestimmt: Q = nf/δ... Wenn eine äußere periodische Kraft auf den Schwingkreis einwirkt, kommt es in ihm zu erzwungenen Schwingungen. Die Amplitude erzwungener Schwingungen nimmt bei Schaltkreisen mit hohem Gütefaktor erheblich zu, wenn die Frequenz des äußeren Einflusses nahe bei eo (Resonanz) liegt. Der Schwingkreis ist einer der Hauptbestandteile resonanter Verstärker. Generatoren und andere elektronische Geräte.
Siehe auch zu diesem Thema: Anwendung von Spannungsresonanz und Stromresonanz
