Berechnung des Heizelements

Um einen der Hauptparameter des Drahtes des Heizelements – Durchmesser d, m (mm) – zu bestimmen, werden zwei Berechnungsmethoden verwendet: gemäß der zulässigen spezifischen Oberflächenleistung PF und anhand der Tabelle der aktuellen Belastungen.
Zulässige spezifische Oberflächenleistung PF= P⁄F,
wobei P die Leistung der Drahtheizung ist, W;
F = π ∙ d ∙ l – Heizfläche, m2; l – Drahtlänge, m.
Nach der ersten Methode
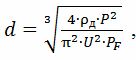
wobei ρd – elektrischer Widerstand des Drahtmaterials bei tatsächlicher Temperatur, Ohm • m; U ist die Heizdrahtspannung V; PF – zulässige Werte der spezifischen Oberflächenleistung für verschiedene Heizgeräte:
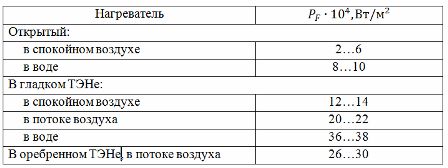
Die zweite Methode verwendet eine Tabelle der aktuellen Belastungen (siehe Tabelle 1), die aus experimentellen Daten zusammengestellt wurde. Um die angegebene Tabelle verwenden zu können, muss die berechnete Heiztemperatur Tp im Verhältnis zur tatsächlichen (oder zulässigen) Temperatur des Leiters Td durch das Verhältnis bestimmt werden:
Tr = Km ∙ Ks ∙ Td,
wobei Km der Installationsfaktor ist, der die konstruktionsbedingte Verschlechterung der Kühlbedingungen des Heizgeräts berücksichtigt; Kc ist der Umgebungsfaktor, der die Verbesserung der Kühlbedingungen des Heizgeräts im Vergleich zu einer stationären Luftumgebung berücksichtigt.
Für ein Heizelement aus spiralförmig verdrilltem Draht gilt Km = 0,8 … 0,9; das gleiche, mit Keramikbasis Km = 0,6 ... 0,7; für einen Draht aus Heizplatten und einigen Heizelementen Km = 0,5 ... 0,6; für einen Leiter aus Elektroboden, Erde und Heizelementen Km = 0,3 ... 0,4. Ein kleinerer Wert von Km entspricht einem Heizkörper mit kleinerem Durchmesser, ein größerer Wert einem größeren Durchmesser.
Bei Betrieb unter anderen Bedingungen als freier Konvektion wird für Heizelemente im Luftstrom Kc = 1,3 … 2,0 angenommen; für Elemente in stillem Wasser Kc = 2,5; im Wasserstrom – Kc = 3,0 … 3,5.
Wenn die Spannung Uph und die Leistung Pf des zukünftigen (entworfenen) Heizgeräts eingestellt werden, dann ist dessen Strom (pro Phase)
Iph = Pph⁄Uph
Anhand des berechneten Werts des Stroms des Heizgeräts für die erforderliche berechnete Temperatur seiner Erwärmung gemäß Tabelle 1 wird der erforderliche Durchmesser des Nichromdrahts d und die erforderliche Länge des Drahts m für die Herstellung des Heizgeräts ermittelt ist berechnet:
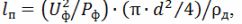
wobei d der ausgewählte Drahtdurchmesser ist, m; ρd ist der spezifische elektrische Widerstand des Leiters bei der tatsächlichen Heiztemperatur, Ohm • m,
ρd = ρ20 ∙ [1 + αp ∙ (Td-20)],
wo αр — Temperaturkoeffizient des Widerstands, 1/OS.
Um die Parameter der Nichrom-Spirale zu bestimmen, nehmen Sie den durchschnittlichen Durchmesser der Windungen D = (6 … 10) ∙ d, die Steigung der Spirale h = (2 … 4) ∙ d,
Anzahl der Züge
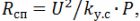
Helixlänge lsp = h ∙ n.
Bei der Berechnung der Heizelemente ist der Widerstand des Spiraldrahtes nach dem Andrücken des Heizelements zu berücksichtigen
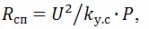
wobei k (y.s) ein Koeffizient ist, der die Verringerung des Widerstands der Spirale berücksichtigt; nach experimentellen Daten ist k(s) = 1,25. Es ist auch zu berücksichtigen, dass die spezifische Oberflächenleistung des Spiraldrahtes 3,5 ... 5-mal größer ist als die spezifische Oberflächenleistung des Rohrheizkörpers.
Bestimmen Sie bei praktischen Berechnungen des Heizelements zunächst die Temperatur seiner Oberfläche Tp = To + P ∙ Rt1,
wobei es sich um die Umgebungstemperatur in °C handelt; P ist die Leistung des Heizelements, W; RT1 – Wärmewiderstand an der Schnittstelle Rohr – Medium, ОC / W.
Dann wird die Temperatur der Wicklung bestimmt: Tsp = To + P ∙ (Rt1 + Rt2 + Rt3),
wobei Rt2 der Wärmewiderstand der Rohrwand ist, ОC / W; RT3 – Wärmewiderstand des Füllstoffs, ОC / W; Rp1 = 1⁄ (α ∙ F), wobei α der Wärmeübergangskoeffizient W / (m ^ 2 • ОС) ist; F – Fläche des Heizgeräts, m2; Rt2 = δ⁄ (λ ∙ F), wobei δ die Wandstärke m ist; λ — Wärmeleitfähigkeit der Wand, W / (m • ОС).
Weitere Informationen zur Einrichtung der Heizelemente finden Sie hier: Heizelemente. Gerät, Auswahl, Bedienung, Anschluss von Heizelementen
Tabelle 1. Tabelle der aktuellen Lasten

Beispiel 1. Berechnen Sie die elektrische Heizung in Form einer Drahtspirale entsprechend der zulässigen spezifischen Oberflächenleistung PF.
Zustand.Heizleistung P = 3,5 kW; Versorgungsspannung U = 220 V; Drahtmaterial – Nichrom Х20Н80 (eine Legierung aus 20 % Chrom und 80 % Nickel), daher beträgt der spezifische elektrische Widerstand des Drahts ρ20 = 1,1 ∙ 10 ^ ( — 6) Ohm • m; Temperaturkoeffizient des Widerstands αр = 16 ∙ 10 ^ (- 6) 1 /ОС; Die Spirale ist offen, in metallischer Form beträgt die Arbeitstemperatur der Spirale Tsp = 400 ОC, PF= 12 ∙ 10 ^ 4 W/m2. Bestimmen Sie d, lp, D, h, n, lp.
Antworten. Spulenwiderstand: R = U ^ 2⁄P = 220 ^ 2⁄3500 = 13,8 Ohm.
Spezifischer elektrischer Widerstand bei Tsp = 400 OS
ρ400 = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (400-20)] = 1,11 ∙ 10 ^ (- 6) Ohm • m.
Finden Sie den Durchmesser des Drahtes:

Aus dem Ausdruck R = (ρ ∙ l) ⁄S erhalten wir l⁄d ^ 2 = (π ∙ R) ⁄ (4 ∙ ρ), woraus sich die Länge des Drahtes ergibt
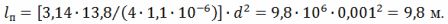
Der durchschnittliche Durchmesser der Spiralwindung beträgt D = 10 ∙ d = 10 ∙ 0,001 = 0,01 m = 10 mm. Spiralsteigung h = 3 ∙ d = 3 ∙ 1 = 3 mm.
Die Anzahl der Windungen der Spirale
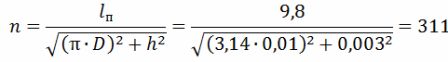
Die Länge der Helix beträgt lsp = h ∙ n = 0,003 ∙ 311 = 0,933 m = 93,3 cm.
Beispiel 2. Berechnen Sie die Struktur der Drahtwiderstandsheizung bei der Bestimmung des Drahtdurchmessers d anhand der Tabelle der Strombelastungen (siehe Tabelle 1).
Zustand. Drahtheizleistung P = 3146 W; Versorgungsspannung U = 220 V; Drahtmaterial — Nichrom Х20Н80 ρ20 = 1,1 ∙ 10 ^ ( — 6) Ohm • m; αp = 16 ∙ 10 ^ (- 6) 1 / ℃; offene Helix im Luftstrom (Km = 0,85, Kc = 2,0); zulässige Betriebstemperatur des Leiters Td = 470 ОС.
Bestimmen Sie den Durchmesser d und die Länge des Drahtes lp.
Antworten.
Tr = Km ∙ Ks ∙ Td = 0,85 ∙ 2 ∙ 470 OS = 800 OS.
Der Auslegungsheizstrom I = P⁄U = 3146⁄220 = 14,3 A.
Gemäß der Tabelle der Strombelastungen (siehe Tabelle 1) bei Tр = 800 ОС und I = 14,3 A finden wir den Durchmesser und Querschnitt des Drahtes d = 1,0 mm und S = 0,785 mm2.
Drahtlänge lp = (R ∙ S) ⁄ρ800,
wobei R = U ^ 2⁄P = 220 ^ 2⁄3146 = 15,3 Ohm, ρ800 = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (800-20) ] = 1,11 ∙ 10 ^ (- 6) Ohm • m, lp = 15,3 ∙ 0,785 ∙ 10 ^ (- 6) ⁄ (1,11 ∙ 10 ^ (- 6)) = 10,9 m.
Außerdem können bei Bedarf, ähnlich wie im ersten Beispiel, D, h, n, lsp definiert werden.
Beispiel 3. Bestimmen Sie die zulässige Spannung des elektrischen Rohrheizkörpers (TEN).
Bedingung... Die Spule des Heizelements besteht aus Nichromdraht mit einem Durchmesser d = 0,28 mm und einer Länge l = 4,7 m. Das Heizelement befindet sich in ruhender Luft mit einer Temperatur von 20 °C. Eigenschaften von Nichrom: ρ20 = 1,1 ∙ 10 ^ (- 6) Ohm • m; αр = 16 ∙ 10 ^ (- 6) 1 / ° C. Die Länge des aktiven Teils des Gehäuses des Heizelements beträgt La = 40 cm.
Das Heizelement ist glatt, Außendurchmesser dob = 16 mm. Wärmeübergangskoeffizient α = 40 W / (m ^ 2 ∙ ° C). Wärmewiderstände: Füllstoff RT3 = 0,3 ОС / W, Gehäusewände Rт2 = 0,002 ОС / W.
Bestimmen Sie, welche maximale Spannung an das Heizelement angelegt werden kann, damit seine Spulentemperatur Tsp 1000 ℃ nicht überschreitet.
Antworten. Heizelementtemperatur des Heizelements
Tsp = To + P ∙ (Rt1 + Rt2 + Rt3),
wobei es sich um die Umgebungslufttemperatur handelt; P ist die Leistung des Heizelements, W; RT1 – Kontaktwärmewiderstand der Rohr-Medium-Grenzfläche.
Leistung des Heizelements P = U ^ 2⁄R,
wobei R der Widerstand der Heizwendel ist.Daher können wir Tsp-To = U ^ 2 / R ∙ (Rt1 + Rt2 + Rt3) schreiben, woraus die Spannung am Heizelement resultiert
U = √ ((R ∙ (Tsp-To)) / (Rt1 + Rt2 + Rt3)).
Finden Sie R = ρ ∙ (4 ∙ l) ⁄ (π ∙ d ^ 2),
wobei ρ1000 = ρ20 ∙ [1 + αp ∙ (T-20)] = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (1000-20)] = 1,12 ∙ 10 ^ ( — 6) Ohm • m.
Dann ist R = 1,12 ∙ 10 ^ (- 6) ∙ (4 ∙ 4,7) ⁄ (3,14 ∙ (0,28 ∙ 10 ^ (- 3)) ^ 2) = 85,5 Ohm.
Kontaktwärmewiderstand RT1 = 1⁄ (α ∙ F),
wobei F die Fläche des aktiven Teils der Hülle des Heizelements ist; F = π ∙ dob ∙ La = 3,14 ∙ 0,016 ∙ 0,4 = 0,02 m2.
Finden Sie Rt1 = 1⁄ (40 ∙ 0,02 = 1,25) OC / W.
Bestimmen Sie die Spannung des Heizelements U = √ ((85,5 ∙ (1000-20)) / (1,25 + 0,002 + 0,3)) = 232,4 V.
Wenn die auf dem Heizelement angegebene Nennspannung 220 V beträgt, beträgt die Überspannung bei Tsp = 1000 OS 5,6 % ∙ Un.
