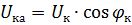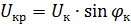Transformator-Kurzschlussmodus
Der Kurzschlussmodus des Transformators ist ein solcher Modus, wenn die Anschlüsse der Sekundärwicklung durch einen Stromleiter mit einem Widerstand gleich Null (ZH = 0) geschlossen sind. Ein Kurzschluss des Transformators während des Betriebs führt zu einem Notbetrieb, da der Sekundärstrom und damit der Primärstrom im Vergleich zum Nennstrom um ein Vielfaches ansteigt. Daher ist in Stromkreisen mit Transformatoren ein Schutz vorgesehen, der den Transformator im Kurzschlussfall automatisch abschaltet.
Unter Laborbedingungen ist es möglich, einen Testkurzschluss des Transformators durchzuführen, bei dem die Anschlüsse der Sekundärwicklung kurzgeschlossen werden und an die Primärwicklung eine Spannung Uk angelegt wird, bei der der Strom in der Primärwicklung dies tut den Nennwert nicht überschreiten (Ik < I1nom). In diesem Fall wird die in Prozent ausgedrückte Spannung Uk mit Ik = I1nom mit uK bezeichnet und als Kurzschlussspannung des Transformators bezeichnet. Es Charakteristik des Transformatorsim Reisepass angegeben.
Daher (%):
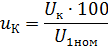
wobei U1nom die Nennprimärspannung ist.
Die Kurzschlussspannung hängt von der höheren Spannung der Transformatorwicklungen ab. Beispielsweise bei einer höheren Spannung von 6-10 kV uK = 5,5 %, bei 35 kV uK = 6,5 ÷ 7,5 %, bei 110 kV uK = 10,5 % usw. Wie Sie sehen, steigt mit steigender Nennspannung auch die Kurzschlussspannung des Transformators.
Wenn die Spannung Uc 5–10 % der Nennprimärspannung beträgt, verringert sich der Magnetisierungsstrom (Leerlaufstrom) um das 10–20-fache oder noch deutlicher. Daher wird dies im Kurzschlussmodus berücksichtigt
Auch der Hauptmagnetfluss F nimmt um den Faktor 10–20 ab und die Leckströme der Wicklungen gleichen sich dem Hauptfluss an.
Denn wenn die Sekundärwicklung des Transformators kurzgeschlossen ist, beträgt die Spannung an seinen Anschlüssen U2 = 0, d. h. usw. pp. weil es die Form annimmt
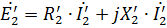
und die Spannungsgleichung für den Transformator wird geschrieben als
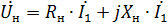
Diese Gleichung entspricht dem in Abb. gezeigten Transformator-Ersatzschaltbild. 1.
Das Vektordiagramm des Kurzschlusstransformators entspricht der Gleichung und dem Diagramm in Abb. 1 ist in FIG. dargestellt. 2. Die Kurzschlussspannung hat aktive und reaktive Komponenten. Der Winkel φk zwischen den Vektoren dieser Spannungen und Ströme hängt vom Verhältnis zwischen den aktiven und reaktiven induktiven Komponenten des Transformatorwiderstands ab.
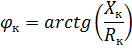
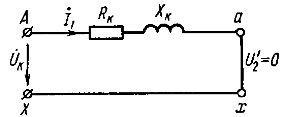
Reis. 1. Ersatzschaltung des Transformators im Kurzschlussfall
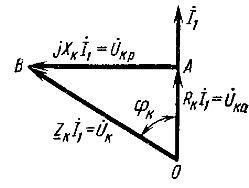
Reis. 2. Vektordiagramm des Transformators bei Kurzschluss
Für Transformatoren mit Nennleistung 5-50 kVA XK / RK = 1 ÷ 2; mit Nennleistung 6300 kVA oder mehr XK / RK = 10 oder mehr. Daher wird angenommen, dass für Hochleistungstransformatoren UK = Ucr und die Impedanz ZK = Xk ist.
Kurzschlusserfahrung.
Dieses Experiment wird wie das Leerlaufexperiment durchgeführt, um die Parameter des Transformators zu bestimmen. Es wird ein Stromkreis aufgebaut (Abb. 3), bei dem die Sekundärwicklung durch eine Metallbrücke oder einen Draht mit einem Widerstand nahe Null kurzgeschlossen wird. An die Primärwicklung wird eine Spannung Uk angelegt, bei der der Strom darin gleich dem Nennwert I1nom ist.
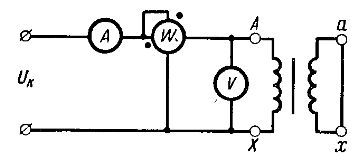
Reis. 3. Schematische Darstellung des Transformator-Kurzschluss-Experiments
Anhand der Messdaten werden folgende Parameter des Transformators ermittelt.
Kurzschlussspannung
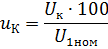
Dabei ist UK die mit einem Voltmeter gemessene Spannung bei I1, = I1nom. Im Kurzschlussmodus ist UK sehr klein, sodass die Leerlaufverluste hunderte Male kleiner sind als bei Nennspannung. Somit können wir davon ausgehen, dass Ppo = 0 ist und die vom Wattmeter gemessene Leistung aufgrund des aktiven Widerstands der Transformatorwicklungen die Verlustleistung Ppk ist.
Beim Strom I1, = I1nom ergeben sich Nennleistungsverluste zur Erwärmung der Wicklungen Rpk.nom, die als elektrische Verluste oder Kurzschlussverluste bezeichnet werden.
Aus der Spannungsgleichung für den Transformator sowie aus dem Ersatzschaltbild (siehe Abb. 1) erhalten wir
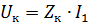
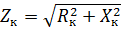
wobei ZK die Impedanz des Transformators ist.
Durch die Messung von Uk und I1 können Sie die Transformatorimpedanz berechnen
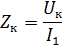
Der Leistungsverlust bei einem Kurzschluss kann durch die Formel ausgedrückt werden
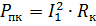
Daher der aktive Widerstand der Transformatorwicklungen
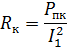
anhand der Wattmeter- und Amperemeterwerte ermittelt werden. Wenn Sie Zk und RK kennen, können Sie den induktiven Widerstand der Wicklungen berechnen:
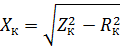
Wenn Sie Zk, RK und Xk des Transformators kennen, können Sie die Kurzschlussspannungen des Hauptdelta (Dreieck OAB in Abb. 2) bilden und auch die aktiven und induktiven Komponenten der Kurzschlussspannung bestimmen:
