Elektrische Filter – Definition, Klassifizierung, Eigenschaften, Haupttypen

Industrielle Energiequellen bieten praktische Möglichkeiten sinusförmige Spannungsverläufe… Gleichzeitig unterscheiden sich periodische Wechselströme und Spannungen in einer Reihe von Fällen stark von harmonischen.

Elektrische Filter können zum Glätten von Spannungswellen in Gleichrichtern, Demodulatoren, die amplitudenmodulierte Hochfrequenzschwingungen in relativ langsame Änderungen der Signalspannung umwandeln, und anderen ähnlichen Geräten verwendet werden.

Im einfachsten Fall können Sie sich auf die serielle Verbindung mit der Last beschränken Induktoren, dessen Widerstand mit zunehmender harmonischer Ordnung zunimmt und für niederfrequente Schwingungen und noch mehr für den konstanten Anteil relativ klein ist. Effektiver ist die Verwendung von U-förmigen, T-förmigen und L-förmigen Filtern.

Grundlegende Definitionen und Klassifizierung elektrischer Filter

Die Selektivität des Filters ist seine Fähigkeit, aus dem gesamten Frequenzspektrum der in seinen Eingang eintretenden Ströme einen bestimmten Frequenzbereich auszuwählen, der dem Nutzsignal innewohnt.

Um eine gute Selektivität zu erreichen, muss der Filter Ströme bei Frequenzen, die dem gewünschten Signal innewohnen, mit minimaler Dämpfung durchlassen und für Ströme bei allen anderen Frequenzen eine maximale Dämpfung aufweisen. In Übereinstimmung mit diesem Filter kann die folgende Definition angegeben werden.

Als elektrischer Filter wird ein vierpoliges Gerät bezeichnet, das Ströme in einem bestimmten Frequenzband mit geringer Dämpfung (Bandbreite) überträgt und Ströme mit Frequenzen außerhalb dieses Bandes – mit hoher Dämpfung oder, wie es üblicherweise heißt, nicht durchlässt (nicht-bandbreite). Übertragungsband).

Je nach Aufbau der Schaltungen werden Filter in Ketten- (Spalten-) und Brückenfilter unterteilt. Kettenfilter sind Filter, die nach T-, P- und L-förmigen Brückenschaltungen aufgebaut sind. Brückenfilter sind Filter, die auf einer Brückenschaltung basieren.

Abhängig von der Art der Elemente werden Filter unterteilt in:

• LC – Elemente davon sind Induktivität und Kapazität;

• RC – Elemente davon sind aktive Widerstände und Kapazitäten;

• Resonator – dessen Elemente Resonatoren sind.

Je nach Vorhandensein der Energiequellen im Filterkreislauf werden diese unterteilt in:

• passiv – keine Energiequellen im Stromkreis enthalten;

• aktiv – enthält Energiequellen im Stromkreis in Form einer Lampe oder eines Kristallverstärkers; manchmal auch aktive Elementfilter genannt.

Für eine vollständige Charakterisierung der Filterleistung ist es notwendig, ihre elektrischen Eigenschaften zu kennen, zu denen die Frequenzabhängigkeiten von Dämpfung, Phasenverschiebung und charakteristischer Impedanz gehören.

Am besten ist ein Filter, der bei einer minimalen Anzahl von Elementen Folgendes aufweist:

• die maximale Steilheit der Dämpfungskennlinie;

• hohe Dämpfung im Nicht-Übertragungsband;

• minimale und konstante Dämpfung im Durchlassbereich;

• maximale Konstanz der charakteristischen Impedanz im Durchlassbereich;

• linearer Phasengang;

• die Möglichkeit einer einfachen und reibungslosen Einstellung des Frequenzbandes und seiner Breite;

• Konstanz der Eigenschaften, die nicht abhängig sind von: Spannungen (Strömen), die am Filtereingang wirken, Temperatur und Luftfeuchtigkeit der Umgebung sowie dem Einfluss äußerer elektrischer und magnetischer Störungen;

• Fähigkeit, in verschiedenen Frequenzbereichen zu arbeiten;

• Größe, Gewicht und Kosten des Filters müssen auf ein Minimum beschränkt werden.

Leider gibt es keinen einzigen Elementarfiltertyp, dessen Eigenschaften alle diese Anforderungen erfüllen. Daher kommen je nach den konkreten Bedingungen solche Filtertypen zum Einsatz, deren Eigenschaften den technischen Anforderungen am besten entsprechen. Sehr oft ist es notwendig, Filter auf komplexe Schaltkreise anzuwenden, die aus elementaren Verbindungen unterschiedlicher Art bestehen.

Die gängigsten Filtertypen

In Abb. 1 zeigt das Diagramm eines einfachen L-förmigen Filters mit Induktivität L und Kondensator C, die zwischen Empfänger rpr und Gleichrichter V geschaltet sind.

Die Wechselströme aller Frequenzen treffen auf einen erheblichen Induktorwiderstand, und ein parallel geschalteter Kondensator leitet die restlichen Hochfrequenzströme entlang des Parallelzweigs weiter. Dadurch werden Spannungswelligkeiten in der Last deutlich reduziert. rNS.

Es können auch Filter verwendet werden, die aus zwei oder mehr ähnlichen Links bestehen. Manchmal werden anstelle von Induktivitäten einfache Filter mit Widerständen verwendet.

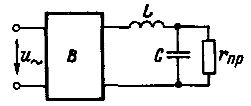
Reis. 1.Der einfachste glättende L-förmige Elektrofilter

Fortschrittlicher sind die von ihnen verwendeten Resonanzfilter Resonanzphänomene.

Wenn die Induktivität und der Kondensator in Reihe geschaltet sind und fwL = 1 / (kwV), hat der Schaltkreis die höchste Leitfähigkeit (aktiv) bei der Frequenz fw und recht hohe Leitfähigkeiten im Frequenzband nahe der Resonanz. Diese Schaltung ist ein einfacher Bandpassfilter.

Wenn Induktor und Kondensator parallel geschaltet sind, weist ein solcher Schaltkreis die niedrigste Leitfähigkeit bei der Resonanzfrequenz und eine relativ niedrige Leitfähigkeit im Frequenzband nahe der Resonanzfrequenz auf. Ein solcher Filter ist ein Sperrfilter für ein bestimmtes Frequenzband.

Um die Leistung eines einfachen Bandpassfilters zu verbessern, kann ein Schema (Abb. 2) verwendet werden, bei dem eine Induktivität und ein Kondensator parallel zueinander parallel zum Empfänger geschaltet sind. Ein solcher Schaltkreis ist außerdem in Resonanz mit der Frequenz der Ziegen abgestimmt und bietet einen sehr hohen Widerstand für Ströme im ausgewählten Frequenzband und einen viel geringeren Widerstand für Ströme anderer Frequenzen.

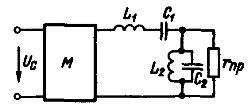
Reis. 2. Schema eines einfachen Bandpassfilters

Ein ähnlicher Filter kann in Modulatoren verwendet werden, die modulierte Schwingungen mit einer bestimmten Frequenz erzeugen. An den Modulator M wird eine niederfrequente Signalspannung Uc angelegt, die in modulierte hochfrequente Schwingungen umgewandelt wird, und der Filter trennt die Spannung von der erforderlichen Frequenz, die der Last rNS zugeführt wird.

Nehmen wir beispielsweise an, dass ein nicht sinusförmiger Wechselstrom durch den Stromkreis fließt und dass sehr große Ströme der dritten und fünften Harmonischen aus der Empfängerstromkurve eliminiert werden sollen.Als nächstes werden wir abwechselnd zwei auf Resonanz abgestimmte Schaltungen für die dritte und fünfte Harmonische in die Schaltung einbinden (Abb. 3, a).

Eine auf Resonanz abgestimmte Impedanz der linken Leitung für eine Frequenz von 3 W ist für diese Frequenz sehr groß und für alle anderen Harmonischen klein; Eine ähnliche Rolle spielt der richtige Schaltkreis, der auf Resonanz für die Frequenz 5w abgestimmt ist. Daher enthält die Stromkurve des Eingangsempfängers fast keine dritten und fünften Harmonischen (Abb. 3, b), die durch die unterdrückt werden Filter.

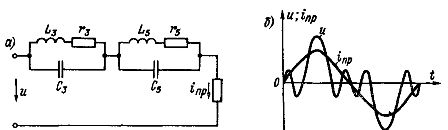
Reis. 3. Schema mit in Reihe geschalteten Resonanzkreisen, die auf Resonanz für die dritte und fünfte Harmonische abgestimmt sind: a – Schaltplan; b – Kurven der Spannung und des Stromkreises sowie des Stromeingangs des Empfängers

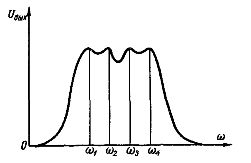
Reis. 4. Ausgangsspannungskurve des Bandpassfilters

In einigen Fällen werden anspruchsvollere Bandpassfilter sowie Grenzfilter eingesetzt, die Schwingungen ab einer bestimmten Frequenz durchlassen oder nicht durchlassen. Solche Filter bestehen aus T-förmigen oder U-förmigen Verbindungen.

Das Funktionsprinzip von Filtern besteht darin, dass im Frequenzband von Frequenzen, beispielsweise einem Bandpassfilter, Resonanz bei n + 1 Frequenzen auftritt, wobei n die Anzahl der Verbindungen ist. Eine Kurve Uout = f (w) für einen solchen Filter bestehend aus drei Anschlüssen ist in Abb. dargestellt. 4. Resonanz tritt bei den Frequenzen w1,w2, w3 und w4 auf.

Siehe auch zu diesem Thema: Leistungsfilter UndEingangs- und Ausgangsfilter für Frequenzumrichter