Einphasiger Wechselstrom
Wechselstrom beziehen
 Wenn der Draht A im durch die beiden Pole des Magneten gebildeten magnetischen Fluss im Uhrzeigersinn gedreht wird (Abb. 1), dann induziert der Draht beim Kreuzen der magnetischen Feldlinien e. d. s, deren Wert durch den Ausdruck bestimmt wird
Wenn der Draht A im durch die beiden Pole des Magneten gebildeten magnetischen Fluss im Uhrzeigersinn gedreht wird (Abb. 1), dann induziert der Draht beim Kreuzen der magnetischen Feldlinien e. d. s, deren Wert durch den Ausdruck bestimmt wird
E = Blvsinα,
Dabei ist B die magnetische Induktion in T, l die Länge des Drahtes in m, v die Geschwindigkeit des Drahtes in m/s und α der Winkel, in dem der Draht die magnetischen Feldlinien kreuzt.
Bleiben B, I und v für diesen Fall konstant, dann ist das induzierte e. usw. c. hängt nur vom Winkel α ab, in dem der Draht das Magnetfeld kreuzt. Wenn sich der Draht an Punkt 1 entlang der Magnetfeldlinien bewegt, beträgt der Wert der induzierten EMK. usw. p wird Null sein, wenn sich der Draht zum Punkt 3 oe bewegt. usw. v. wird von größter Bedeutung sein, da die Kraftlinien vom Leiter in der dazu senkrechten Richtung gekreuzt werden und schließlich, z.B. usw. v. wird wieder Null erreichen, wenn der Draht zum Punkt 5 bewegt wird.
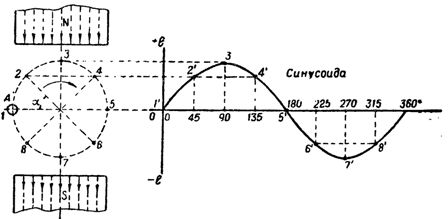
Reis. 1. Änderung des induzierten e. usw. pp. in einem Draht, der sich in einem Magnetfeld dreht
An den Zwischenpunkten 2 und 4, in denen der Draht die Kraftlinien in einem Winkel α = 45° kreuzt, beträgt der Wert der induzierten EMK. usw. c. wird entsprechend geringer sein als an Punkt 3. Wenn also der Draht von Punkt 1 nach Punkt 5 gedreht wird, also um 180°, wird der induzierte e. usw. v. ändert sich von Null auf Maximum und zurück auf Null.
Es ist ganz offensichtlich, dass bei einer weiteren Drehung des Drahtes A um einen Winkel von 180° (durch die Punkte 6, 7, 8 und 1) die Art der Änderung des induzierten e. usw. p. wird derselbe sein, aber seine Richtung ändert sich in die entgegengesetzte Richtung, da der Draht die Magnetfeldlinien bereits unter dem anderen Pol kreuzt, was gleichbedeutend damit ist, sie in der entgegengesetzten ersten Richtung zu kreuzen.
Wenn der Draht um 360° gedreht wird, wird daher das induzierte e. usw. v. ändert nicht nur ständig seine Größe, sondern ändert auch zweimal seine Richtung.
Wenn der Draht auf einen gewissen Widerstand geschlossen ist, erscheint der Draht Elektrizität, auch in Größe und Richtung variierend.
Elektrischer Strom, der sich ständig in Größe und Richtung ändert, wird Wechselstrom genannt.
Was ist eine Sinuswelle?
Die Art der Änderung, z. usw. (Strom) für eine Drahtwindung werden zur besseren Übersichtlichkeit grafisch anhand einer Kurve dargestellt. Da der Wert von e. usw. c. proportional zu sinα, dann ist es nach Einstellung bestimmter Winkel möglich, mit Hilfe von Tabellen den Wert des Sinus jedes Winkels zu bestimmen und im entsprechenden Maßstab eine Kurve für die Änderung von e zu konstruieren. usw. c. Dazu tragen wir auf der horizontalen Achse die Drehwinkel des Drahtes beiseite und auf der vertikalen Achse im entsprechenden Maßstab das induzierte e. usw. mit
Wenn zuvor in Abb. angegeben.1. Verbinden Sie die Punkte mit einer glatten gekrümmten Linie, dann erhalten Sie eine Vorstellung von der Größe und Art der Änderung des induzierten e. usw. (Strom) an jeder Position des Leiters in einem Magnetfeld. Aufgrund der Tatsache, dass der Wert des induzierten e. usw. p. wird zu jedem Zeitpunkt durch den Sinus des Winkels bestimmt, in dem der Draht das in Abb. gezeigte Magnetfeld kreuzt. 1 Kurve wird Sinuskurve genannt, und e. usw. s. – sinusförmig.
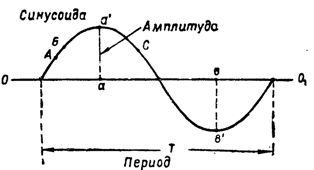
Reis. 2. Die Sinuskurve und ihre charakteristischen Werte
Die Änderungen, die wir uns angesehen haben, z. usw. c. sinusförmig entsprechen der Drehung des Drahtes in einem Magnetfeld in einem Winkel von 360°. Wenn der Draht um die nächsten 360° gedreht wird, ändern sich die induzierten e. usw. s.(und Strom) erscheinen wieder in einer Sinuswelle, das heißt, sie wiederholen sich periodisch.
Dementsprechend verursacht durch dieses e. usw. c. heißt elektrischer Strom sinusförmiger Wechselstrom... Es ist ganz offensichtlich, dass sich die Spannung, die wir an den Enden von Draht A messen können, bei Vorhandensein eines geschlossenen externen Stromkreises ebenfalls sinusförmig ändert.
Wechselstrom, der durch Drehen eines Drahtes in einem magnetischen Fluss oder eines Systems von in einer Spule verbundenen Drähten entsteht, wird als einphasiger Wechselstrom bezeichnet.
Sinusförmige Wechselströme werden in der Technik am häufigsten eingesetzt. Es gibt jedoch Wechselströme, die sich nicht nach dem Sinusgesetz ändern. Solche Wechselströme werden als nicht sinusförmig bezeichnet.
Siehe auch: Was ist Wechselstrom und wie unterscheidet er sich vom Gleichstrom?
Amplitude, Periode, Frequenz des einphasigen Wechselstroms
Aktuelle Stärke, sich entlang einer Sinuskurve ändernd, ändert sich kontinuierlich. Wenn also am Punkt A (Abb. 2) der Strom gleich 3a ist, dann ist er am Punkt B bereits größer.An einem anderen Punkt der Sinuskurve, zum Beispiel am Punkt C, hat der Strom nun einen neuen Wert und so weiter.
Die Stärke des Stroms zu bestimmten Zeitpunkten, wenn er sich entlang einer Sinuskurve ändert, wird als Momentanstromwert bezeichnet.
Der größte Momentanwert eines einphasigen Wechselstroms wird aufgerufen, wenn er sich entlang einer Sinusamplitude ändert... Es ist leicht zu erkennen, dass der Strom bei einer Drahtwindung seinen Amplitudenwert zweimal erreicht. Einer der Werte von aa 'ist positiv und wird von der 001-Achse nach oben gezeichnet, und der andere Wert von bv ' ist negativ und wird von der Achse nach unten gezeichnet.
Die Zeit, während der das induzierte e. usw. (bzw. die aktuelle Kraft) durchläuft den gesamten Änderungszyklus, den sogenannten Monatszyklus T (Abb. 2). Der Zeitraum wird normalerweise in Sekunden gemessen.
Der Kehrwert der Periode wird als Frequenz (f) bezeichnet. Mit anderen Worten, Wechselstromfrequenz ist die Anzahl der Perioden pro Zeiteinheit, d.h. in Sekunden. Wenn also beispielsweise ein Wechselstrom innerhalb von 1 Sekunde zehnmal die gleichen Werte und die gleiche Richtung annimmt, dann beträgt die Frequenz eines solchen Wechselstroms 10 Perioden pro Sekunde.
Zur Messung der Frequenz wird anstelle der Anzahl der Perioden pro Sekunde eine Einheit namens Hertz (Hertz) verwendet. Eine Frequenz von 1 Hertz entspricht einer Frequenz von 1 lps/s. Bei der Messung hoher Frequenzen ist es praktischer, eine Einheit zu verwenden, die 1000-mal größer als Hertz ist, d. h. Kilohertz (kHz) oder 1.000.000-mal größer als Hertz – Megahertz (mhz).
In der Technik verwendete Wechselströme lassen sich je nach Frequenz in niederfrequente Ströme und hochfrequente Ströme unterteilen.

AC-Effektivwert
Gleichstrom, der durch den Draht fließt, erwärmt ihn. Wenn Sie Wechselstrom durch den Draht leiten, erwärmt sich auch der Draht.Das ist verständlich, denn obwohl der Wechselstrom ständig seine Richtung ändert, hängt die Wärmeabgabe überhaupt nicht von der Stromrichtung im Draht ab.
Wenn Wechselstrom durch eine Glühbirne fließt, leuchtet ihr Glühfaden. Bei einer Standard-Wechselstromfrequenz von 50 Hz tritt kein Flackern des Lichts auf, da der Glühfaden der Glühbirne aufgrund seiner thermischen Trägheit keine Zeit zum Abkühlen hat, wenn der Strom im Stromkreis Null ist. Die Verwendung von Wechselstrom mit einer Frequenz von weniger als 50 Hz zur Beleuchtung ist mittlerweile unerwünscht, da unangenehme, augenermüdende Schwankungen in der Intensität der Glühbirne auftreten.
Wenn wir die Gleichstrom-Analogie fortsetzen, können wir davon ausgehen, dass ein Wechselstrom, der durch einen Draht fließt, um ihn herum erzeugt wird Magnetfeld. Tatsächlich erzeugt Wechselstrom kein Magnetfeld, da das von ihm erzeugte Magnetfeld jedoch auch in Richtung und Stärke variabel ist.
Ein Wechselstrom ändert sich ständig sowohl in seiner Größe als auch in seiner RichtungNS. Natürlich stellt sich die Frage, wie man die Variable T gut messen kann und welchen Wert ihr Wert bei der Änderung entlang einer Sinuskurve als Ursache dieser oder jener Aktion annehmen sollte.
C Dazu wird Wechselstrom in seiner Wirkung mit Gleichstrom verglichen, dessen Wert während des Versuchs unverändert bleibt.

Angenommen, ein Gleichstrom fließt durch einen Draht mit einem konstanten Widerstand von 10 A und es wird festgestellt, dass der Draht auf eine Temperatur von 50 ° erhitzt wird.Wenn wir nun durch denselben Draht keinen Gleichstrom, sondern einen Wechselstrom leiten und dessen Wert (z. B. mit einem Rheostat) so wählen, dass der Draht auch auf eine Temperatur von 50 ° erhitzt wird, dann in In diesem Fall können wir sagen, dass die Wirkung von Wechselstrom gleich der Wirkung von Gleichstrom ist.
Erhitzt man den Draht in beiden Fällen auf die gleiche Temperatur, so zeigt sich, dass der Wechselstrom in einer Zeiteinheit die gleiche Wärmemenge im Draht abgibt wie der Gleichstrom.
Ein sinusförmiger Wechselstrom, der bei einem gegebenen Widerstand pro Zeiteinheit die gleiche Wärmemenge abgibt wie ein Gleichstrom, dessen Größe einem Gleichstrom entspricht. Dieser Stromwert wird als Effektivwert (Id) oder Effektivwert des Wechselstroms bezeichnet. . Daher beträgt in unserem Beispiel der Effektivwert des Wechselstroms 10 A... In diesem Fall werden die maximalen (Spitzen-)Stromwerte die Durchschnittswerte in der Größe übertreffen.
Erfahrungen und Berechnungen zeigen, dass die Effektivwerte des Wechselstroms um das √2 (1,41)-fache kleiner sind als seine Amplitudenwerte. Wenn daher der Spitzenwert des Stroms bekannt ist, kann der effektive Wert des Stroms Id bestimmt werden, indem die Amplitude des Stroms Ia durch √2 dividiert wird, d. h. Id = Aza/√2
Wenn umgekehrt der Effektivwert des Stroms bekannt ist, kann der Spitzenwert des Stroms berechnet werden, d. h. Ia = Azd√2
Die gleichen Beziehungen gelten für die Amplitude und die Effektivwerte von e. usw. v. und Spannungen: Einheit = Ea /√2, Ud = Uа/√2
Messgeräte zeigen meist die tatsächlichen Werte an, daher wird bei der Notation meist der Index „d“ weggelassen, den man aber nicht vergessen sollte.
Impedanz in Wechselstromkreisen
Wenn induktive und kapazitive Verbraucher an den Wechselstromkreis angeschlossen werden, müssen sowohl die Wirk- als auch die Reaktanz berücksichtigt werden (Reaktanz tritt auf, wenn ein Kondensator eingeschaltet oder eingeschaltet ist). Drosseln in einem Wechselstromkreis). Daher ist es bei der Bestimmung des durch einen solchen Verbraucher fließenden Stroms erforderlich, die Versorgungsspannung durch die Impedanz des Stromkreises (Verbrauchers) zu dividieren.
Die Impedanz (Z) eines einphasigen Wechselstromkreises wird durch die folgende Formel bestimmt:
Z = √(R2 + (ωL — 1 / ωC)2
Dabei ist R der aktive Widerstand des Stromkreises in Ohm, L die Induktivität des Stromkreises in Henry, C die Kapazität des Stromkreises (Kondensator) in Farad und ω die Kreisfrequenz des Wechselstroms.
In Wechselstromkreisen kommen unterschiedliche Verbraucher zum Einsatz, bei denen entweder die drei Werte R, L, C oder nur einige davon berücksichtigt werden müssen. Dabei ist die Kreisfrequenz des Wechselstroms zu berücksichtigen.
Für einige Benutzer können nur die Werte von R und L bei den entsprechenden Eckfrequenzwerten berücksichtigt werden, beispielsweise bei einer Wechselstromfrequenz von 50 Hz Magnetspule oder es kann nur davon ausgegangen werden, dass die Generatorwicklung einen aktiven und induktiven Widerstand enthält. Mit anderen Worten: Die Kapazität kann in diesem Fall vernachlässigt werden. Dann kann die Wechselstromimpedanz eines solchen Benutzers mit der Formel berechnet werden:
Z = √(R2 + ω2L2)
Wird eine solche Spule oder eine für Wechselstrombetrieb ausgelegte Spule an einen Gleichstrom gleicher Spannung angeschlossen, fließt ein sehr großer Strom durch die Spule, was zu erheblicher Wärmeentwicklung führen kann und die Isolierung der Spule beschädigt werden kann Im Gegenteil: Ein kleiner Strom fließt durch eine Spule, die für den Betrieb in einem Gleichstromkreis ausgelegt und an einen Wechselstromkreis mit derselben Spannung angeschlossen ist, und das Gerät, in dem diese Spule verwendet wird, führt nicht die erforderliche Wirkung aus.
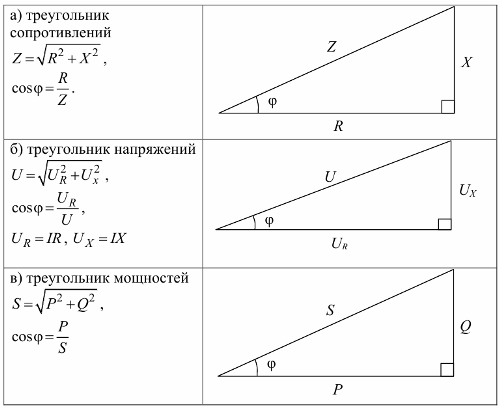
Widerstandsdreieck, Spannungsdreieck und Leistungsdreieck: