Impulsstrom

In verschiedenen elektronischen Geräten, zum Beispiel in Elektronik- und Halbleitergeräten, also in Verstärkern, Gleichrichtern, Radios, Generatoren, Fernsehgeräten, aber auch in Kohlemikrofonen, Telegrafen und vielen anderen Geräten, werden häufig Welligkeitsströme und -spannungen verwendet… Der Reihe nach Um die Überlegung nicht noch einmal zu wiederholen, sprechen wir hier nur von Strömen, aber alles, was mit Strömen zusammenhängt, gilt auch für Spannungen.

Pulsierende Ströme, die eine konstante Richtung haben, aber ihren Wert ändern, können unterschiedlich sein. Manchmal ändert sich der aktuelle Wert vom höchsten zum niedrigsten Wert ungleich Null. In anderen Fällen wird der Strom auf Null reduziert. Wenn Gleichstromkreis bei einer bestimmten Frequenz unterbrochen wird, dann fließt für einige Zeitintervalle kein Strom im Stromkreis.

In Abb. 1 zeigt Diagramme verschiedener Wellenströme. In Abb. 1, a, b, die Änderung der Ströme erfolgt gemäß Sinuskurve, aber diese Ströme sollten nicht als sinusförmige Wechselströme betrachtet werden, da sich die Richtung (das Vorzeichen) des Stroms nicht ändert. In Abb.In Abb. 1, c zeigt einen Strom, der aus einzelnen Impulsen besteht, also kurzlebigen „Stromstößen“, die durch mehr oder weniger lange Pausen voneinander getrennt sind, und wird oft als gepulster Strom bezeichnet. Verschiedene gepulste Ströme unterscheiden sich voneinander in der Form und Dauer der Impulse sowie in der Wiederholungsrate.

Es ist zweckmäßig, einen pulsierenden Strom jeglicher Art als die Summe zweier Ströme – Gleich- und Wechselströme – zu betrachten, die als Term- oder Komponentenströme bezeichnet werden. Jeder pulsierende Strom hat Gleich- und Wechselstromanteile. Das kommt vielen seltsam vor. Tatsächlich ist ein pulsierender Strom ein Strom, der ständig in eine Richtung fließt und seinen Wert ändert.

Woran erkennt man, dass es Wechselstrom enthält, der die Richtung ändert? Wenn jedoch zwei Ströme – Gleich- und Wechselströme – gleichzeitig durch denselben Draht fließen, stellt sich heraus, dass in diesem Draht ein pulsierender Strom fließt (Abb. 2). In diesem Fall sollte die Amplitude des Wechselstroms den Wert des Gleichstroms nicht überschreiten. Gleich- und Wechselstrom können nicht getrennt durch den Draht fließen. Sie tragen zu einem allgemeinen Elektronenfluss bei, der alle Eigenschaften eines pulsierenden Stroms aufweist.

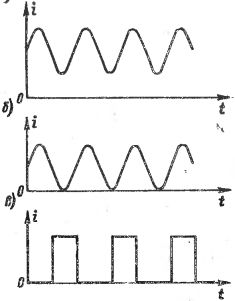
Reis. 1. Diagramme verschiedener Wellenströme

Die Addition von Wechsel- und Gleichströmen kann grafisch dargestellt werden. In Abb. In Abb. 2 zeigt die Diagramme eines Gleichstroms von 15 mA und eines Wechselstroms mit einer Amplitude von 10 mA. Wenn wir die Werte dieser Ströme für einzelne Zeitpunkte summieren und dabei die Richtungen (Vorzeichen) der Ströme berücksichtigen, erhalten wir das in Abb. 1 dargestellte Wellenstromdiagramm. 2 mit fetter Linie. Dieser Strom variiert von einem Tiefstwert von 5 mA bis zu einem Höchstwert von 25 mA.

Die betrachtete Addition der Ströme bestätigt die Gültigkeit der Darstellung des pulsierenden Stroms als Summe von Gleich- und Wechselströmen. Die Richtigkeit dieser Darstellung wird auch dadurch bestätigt, dass es mit Hilfe einiger Geräte möglich ist, die Komponenten dieses Stroms voneinander zu trennen.

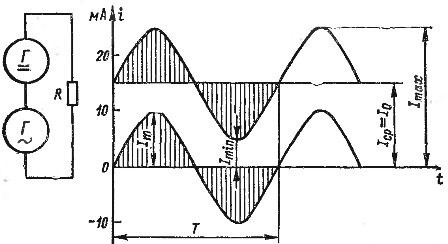
Reis. 2. Erzielen eines pulsierenden Stroms durch Addition von Gleich- und Wechselstrom.

Es ist zu betonen, dass jeder Strom immer als Summe mehrerer Ströme dargestellt werden kann. Beispielsweise kann ein Strom von 5 A als Summe der Ströme 2 und 3 A betrachtet werden, die in eine Richtung fließen, oder als Summe der Ströme 8 und 3 A, die in verschiedene Richtungen fließen, also mit anderen Worten als Differenz zwischen den Strömen 8 und 3 A. Es ist nicht schwierig, andere Kombinationen von zwei oder mehr Strömen zu finden, die insgesamt 5 A ergeben.

Hier besteht eine völlige Ähnlichkeit mit dem Prinzip der Addition und Zerlegung von Kräften. Wirken auf einen Gegenstand zwei gleichgerichtete Kräfte, so können diese durch eine gemeinsame Kraft ersetzt werden. Gegenläufig wirkende Kräfte können durch eine Einheitsdifferenz ersetzt werden. Umgekehrt kann eine gegebene Kraft immer als Summe entsprechender gleichgerichteter Kräfte oder als Differenz entgegengesetzt gerichteter Kräfte betrachtet werden.

Es ist nicht erforderlich, Gleich- oder Sinuswechselströme in Teilströme zu zerlegen. Wenn wir den pulsierenden Strom durch die Summe von Gleich- und Wechselströmen ersetzen, ist es durch die Anwendung der bekannten Gesetze von Gleich- und Wechselströmen auf diese Komponentenströme möglich, viele Probleme zu lösen und die notwendigen Berechnungen im Zusammenhang mit pulsierendem Strom durchzuführen.

Das Konzept des pulsierenden Stroms als Summe von Gleich- und Wechselströmen ist konventionell.Natürlich kann nicht davon ausgegangen werden, dass in bestimmten Zeitabständen tatsächlich Gleich- und Wechselstrom entlang des Drahtes aufeinander zufließen. Tatsächlich gibt es keine zwei entgegengesetzten Elektronenflüsse.

In Wirklichkeit ist ein pulsierender Strom ein einzelner Strom, der seinen Wert im Laufe der Zeit ändert. Es ist richtiger zu sagen, dass die pulsierende Spannung oder pulsierende EMF als Summe der konstanten und variablen Komponenten dargestellt werden kann.

In FIG. 2 zeigt, wie algebraisch die konstante EMK eines Generators zur variablen EMK eines anderen Generators addiert wird. Infolgedessen haben wir eine pulsierende EMF, die den entsprechenden pulsierenden Strom verursacht. Bedingt kann jedoch davon ausgegangen werden, dass eine konstante EMF einen Gleichstrom im Stromkreis erzeugt und eine alternierende EMF einen Wechselstrom, der in der Summe einen pulsierenden Strom bildet.

Jeder pulsierende Strom kann durch die Maximal- und Minimalwerte von Itax und Itin sowie seine konstanten und variablen Komponenten charakterisiert werden. Der konstante Anteil wird mit I0 bezeichnet. Handelt es sich bei der Wechselkomponente um einen Sinusstrom, so wird seine Amplitude mit It bezeichnet (alle diese Größen sind in Abb. 2 dargestellt).

Es sollte nicht mit It und Itax verwechselt werden. Außerdem sollte der Maximalwert der Stromwelle Imax nicht als Amplitude bezeichnet werden. Der Begriff Amplitude bezieht sich üblicherweise nur auf Wechselströme. Bezüglich des pulsierenden Stroms können wir nur über die Amplitude seines variablen Anteils sprechen.

Der konstante Anteil des pulsierenden Stroms kann als sein Durchschnittswert Iav, also als arithmetischer Mittelwert, bezeichnet werden. Wenn wir tatsächlich die Änderungen in einer Periode des pulsierenden Stroms betrachten, die in Abb.In Abb. 2 ist Folgendes deutlich zu erkennen: In der ersten Halbwelle werden dem 15-mA-Strom durch Variation des Stromanteils mehrere Werte hinzugefügt, die von 0 auf 10 mA und wieder zurück auf 0 variieren, und in der zweiten Hälfte -Zyklus werden von den aktuellen 15 mA genau die gleichen Stromwerte subtrahiert.

Daher ist der Strom von 15 mA wirklich der Durchschnittswert. Da Strom die Übertragung elektrischer Ladungen durch den Drahtquerschnitt ist, ist Iav der Wert eines solchen Gleichstroms, der in einer Periode (oder über eine ganze Anzahl von Perioden) die gleiche Strommenge transportiert wie dieser pulsierende Strom .

Bei sinusförmigem Wechselstrom beträgt der Wert von Iav pro Periode Null, da die Strommenge, die in einer Halbperiode durch den Leiterquerschnitt fließt, gleich der Strommenge ist, die während einer anderen Halbperiode in die entgegengesetzte Richtung fließt. In den Stromdiagrammen, die die Abhängigkeit des Stroms i von der Zeit t zeigen, wird die vom Strom transportierte Elektrizitätsmenge durch die Fläche der durch die Stromkurve begrenzten Figur ausgedrückt, da die Elektrizitätsmenge durch die bestimmt wird Produkt, das es.

Bei einem sinusförmigen Strom sind die Flächen der positiven und negativen Halbwellen gleich. Bei dem pulsierenden Strom in Abb. Wie in 2 dargestellt, wird während der ersten Halbzeit die von der AC-Komponente transportierte Strommenge zur vom aktuellen Iav transportierten Strommenge addiert (schattierter Bereich in der Abbildung). Und im zweiten Halbzyklus wird genau die gleiche Menge Strom entnommen. Dadurch wird über den gesamten Zeitraum die gleiche Strommenge übertragen wie bei einem einzelnen Gleichstrom Iav, d. h. die Fläche des Rechtecks ​​Iav T ist gleich der durch die Wellenstromkurve begrenzten Fläche.

Somit wird die konstante Komponente oder der Durchschnittswert des Stroms durch die Übertragung elektrischer Ladungen durch den Drahtquerschnitt bestimmt.

Die aktuelle Gleichung in Abb. 2 sollte natürlich in der folgenden Form geschrieben werden:

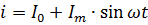
Die Leistung des pulsierenden Stroms muss als Summe der Leistungen seiner Komponentenströme berechnet werden. Wenn zum Beispiel der in Abb. 2, durchläuft ein Widerstand den Widerstandswert R, dann beträgt seine Leistung

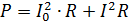
wobei I = 0,7Im der Effektivwert der variablen Komponente ist.

Sie können das Konzept des Effektivwerts des Wellenstroms Id einführen. Die Leistung wird wie gewohnt berechnet:

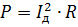
Wenn wir diesen Ausdruck mit dem vorherigen gleichsetzen und ihn mit R reduzieren, erhalten wir:

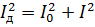
Die gleichen Beziehungen können für Spannungen erhalten werden.