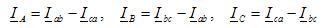Berechnung von Drehstromkreisen

Kette dreiphasiger Wechselstrom besteht aus einer dreiphasigen Stromversorgung, einem dreiphasigen Verbraucher und den dazwischen liegenden Kommunikationsleitungen.

Eine symmetrische dreiphasige Versorgung kann als drei einphasige Versorgungen dargestellt werden, die mit derselben Frequenz, derselben Spannung und einem zeitlichen Phasenwinkel von 120 ° arbeiten. Diese Quellen können in Stern- oder Dreieckschaltung angeschlossen sein.

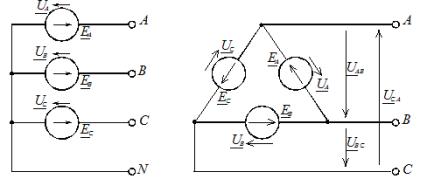
Bei einer Sternschaltung wird der bedingte Anfang der Phasen zum Verbinden von drei linearen Leitern A, B, C verwendet und die Enden der Phasen werden an einem Punkt vereint, der als Sternpunkt der Stromquelle (Dreiphasengenerator) bezeichnet wird oder Transformator). An diesen Punkt kann ein Neutralleiter N angeschlossen werden. Das Sternschaltbild der Stromquelle ist in Abbildung 1, a dargestellt.

Reis. 1. Anschlusspläne der Stromversorgungsphasen: a – Stern; b – Dreieck

Die Spannung zwischen Außenleiter und Neutralleiter wird als Phase und zwischen Außenleitern als Leitung bezeichnet (weitere Einzelheiten finden Sie hier – Netz- und Phasenspannung).

V integrierte Form Die Einträge der Ausdrücke für die Phasenspannungen lauten:

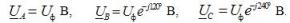
Die entsprechenden Netzspannungen bei Sternschaltung:

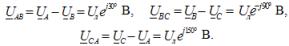
Dabei ist Uf der Phasenspannungsmodul der Stromquelle und Ul der Netzspannungsmodul. In einem symmetrischen Dreiphasensystem besteht bei Sternschaltung der Quellenphasen ein Zusammenhang zwischen diesen Spannungen:

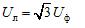
Wenn die Phasen mit einem Dreieck verbunden sind, werden die Phasenstromversorgungen in einer geschlossenen Schleife in Reihe geschaltet (Abbildung 1, b).

Von den Punkten, an denen die Quellen miteinander kombiniert werden, werden drei lineare Drähte A, B, C herausgeführt, die zur Last führen. Aus Abbildung 1, b ist ersichtlich, dass die Ausgänge der Phasenquellen mit linearen Drähten verbunden sind und daher, wenn die Phasen der Quelle durch ein Dreieck verbunden sind, die Phasenspannungen gleich linear sind. In diesem Fall gibt es keinen Neutralleiter.

Eine Last kann an eine dreiphasige Versorgung angeschlossen werden. Eine dreiphasige Last kann hinsichtlich Größe und Beschaffenheit symmetrisch und asymmetrisch sein.

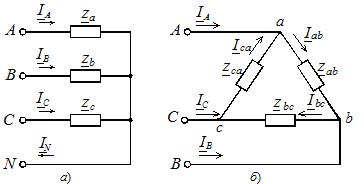
Bei einer symmetrischen Belastung sind die komplexen Widerstände der drei Phasen gleich, sind diese Widerstände unterschiedlich, liegt eine unsymmetrische Belastung vor. Die Lastphasen können unabhängig vom Quellenanschlussschema durch Stern oder Dreieck miteinander verbunden werden (Abbildung 2).

Reis. 2. Phasenanschlusspläne laden

Die Sternschaltung kann mit oder ohne Neutralleiter erfolgen (siehe Abbildung 2, a). Durch das Fehlen eines Neutralleiters entfällt die starre Verbindung der Lastspannung mit der Versorgungsspannung und bei asymmetrischer Phasenlast sind diese Spannungen einander nicht gleich.Zur Unterscheidung haben wir uns darauf geeinigt, in den Buchstabenbezeichnungsindizes der Versorgungsspannungen und -ströme Großbuchstaben und in den lastspezifischen Parametern Kleinbuchstaben zu verwenden.

Der Algorithmus zur Analyse eines Drehstromkreises hängt vom Lastanschlussschema, den Ausgangsparametern und dem Zweck der Berechnung ab.

Die Zwei-Knoten-Methode dient zur Ermittlung der Phasenspannungen bei einer unsymmetrischen Sternlast ohne Neutralleiter. Nach dieser Methode beginnt die Berechnung mit der Bestimmung der Spannung UN zwischen den Sternpunkten der Versorgung und der Last, der sogenannten Neutralabweichungsspannung:

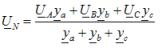
wobei ya, yb, yc – zulässige Werte der entsprechenden Lastphasen in komplexer Form

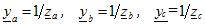
Die Spannungen an den Phasen einer unsymmetrischen Last ergeben sich aus den folgenden Ausdrücken:

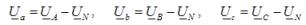
Im Sonderfall der Lastunsymmetrie, wenn in einer der Lastphasen in Abwesenheit eines Neutralleiters ein Kurzschluss auftritt, ist die Neutralvorspannung gleich der Phasenspannung der Versorgung der Phase, in der der Kurzschluss aufgetreten ist geschah.

Die Spannung an der geschlossenen Phase der Last ist Null und an den anderen beiden ist sie numerisch gleich der Netzspannung. Nehmen wir beispielsweise an, dass in Phase B ein Kurzschluss auftritt. Die neutrale Vorspannung beträgt in diesem Fall UN = UB. Dann die Phasenspannungen an der Last:

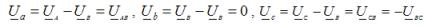
Phasenströme in der Last, sie sind auch Außenleiterströme für jede Art von Last:

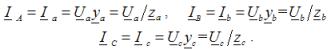
Bei den Aufgaben zur Berechnung von Drehstromkreisen werden drei Möglichkeiten zum Anschluss von Drehstromverbrauchern mit einem Stern betrachtet: Anschluss an einen Neutralleiter bei Vorhandensein von Verbrauchern in drei Phasen, Anschluss an einen Neutralleiter bei Fehlen von Verbrauchern in einer Phase der Phasen und Anschluss ohne Neutralleiter mit Kurzschluss in einer der Lastphasen...

In der ersten und zweiten Variante liegen die entsprechenden Phasenspannungen der Versorgung an den Lastphasen und die Phasenströme in der Last werden durch die oben genannten Formeln ermittelt.

In der dritten Variante ist die Spannung der Lastphasen ungleich der Phasenspannung der Einspeisung und wird anhand der Abhängigkeiten ermittelt

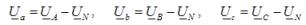
Die Ströme in zwei nicht kurzgeschlossenen Phasen werden nach dem Ohmschen Gesetz als Bruchteil der Division der Phasenspannung durch die Impedanz der jeweiligen Phase bestimmt. Der Kurzschlussstrom wird anhand einer Gleichung ermittelt, die auf basiert Kirchhoffs erstes Gesetzfür den Sternpunkt der Last zusammengestellt.

Für das obige Beispiel eines Kurzschlusses der Phase B:

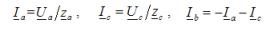
Für jede Lastart sind die dreiphasigen Wirk- und Blindleistungen gleich der Summe der Wirk- und Blindleistungen der einzelnen Phasen. Um diese Phasenleistungen zu bestimmen, können Sie den Ausdruck verwenden

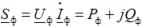
wobei Uf,Azf der Komplex aus der Spannung und dem Komplex der gekoppelten Ströme in der Lastphase ist; Pf, Qf – Wirk- und Blindleistung in der Lastphase.

Dreiphasige Wirkleistung: P = Pa + Pb + Pc

Dreiphasige Blindleistung: Q = Qa + Qb + Vc

Dreiphasige Scheinleistung:

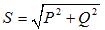
Wenn Verbraucher durch ein Dreieck verbunden sind, hat die Schaltung die in Abbildung 2, b gezeigte Form. In diesem Modus ist der Phasenanschluss der symmetrischen Stromversorgung unerheblich.

An den Lastphasen werden Spannungen zwischen den Stromversorgungsleitungen erfasst. Die Phasenströme in der Last werden mit bestimmt Ohmsches Gesetz für einen Abschnitt eines StromkreisesAzf = Uf /zf, wobei Uf die Phasenspannung in der Last ist (entsprechend der Netzspannung der Stromquelle); zf ist der Gesamtwiderstand der entsprechenden Phase der Last.

Ströme in linearen Leitern werden durch Phasenströme basierend auf dem ersten Kirchhoffschen Gesetz für jeden Knoten (Punkte a, b, c) des in Abbildung 2, b gezeigten Stromkreises bestimmt: