Schaltungstopologien – Grundkonzepte

Ein Stromkreis besteht aus einer Reihe von Geräten (Elementen) und ihren Verbindungsdrähten, durch die ein elektrischer Strom fließen kann. Alle Elemente elektrischer Schaltkreise teilen sich im Passiv und Aktiv.

Aktive Elemente wandeln verschiedene Energiearten (mechanische, chemische, Licht usw.) in elektrische Energie um. In passiven Geräten wird elektrische Energie in andere Energiearten umgewandelt. Aktive Elemente werden als Quellen bezeichnet, passive als Verbraucher oder Empfänger.

In der Schaltungstheorie werden idealisierte Modelle elektrischer Elemente betrachtet. Dies macht die Beschreibung der Elemente so einfach wie möglich. Komplexere, reale Elemente werden aus einer Reihe idealisierter Elemente modelliert.

Die wichtigsten passiven Elemente elektrischer Schaltkreise sind Widerstand (Widerstandselement), Induktor (induktives Element) und Kondensator (kapazitives Element). Elemente werden in einem Stromkreis installiert, um Spannung und Strom mit einem bestimmten Wert und einer bestimmten Form zu erzeugen (siehe – Stromkreis und seine Elemente).

Ein Stromkreis besteht aus Zweigen und Knoten. Zweig — Dies ist ein Abschnitt eines Stromkreises (Stromkreis), durch den der gleiche Strom fließt. Ein Knoten — Verbindung von drei oder mehr Zweigen. Im Schaltplan ist der Knoten durch einen Punkt gekennzeichnet (Abb. 1).

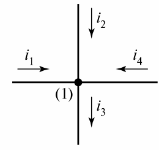
Reis. 1. Definieren Sie den Knoten im Diagramm

Bei Bedarf werden die Knoten des Diagramms von links nach rechts von oben nach unten nummeriert.

In Abb. 2 zeigt den ohmsch-kapazitiven Zweig, in dem der Strom iC fließt.

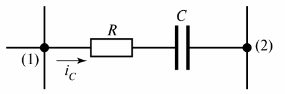
Reis. 2. Resistiv-kapazitiver Zweig

Eine andere Definition eines Zweigs kann gegeben werden – es ist ein Abschnitt einer Schaltung zwischen zwei benachbarten Knoten (Knoten (1) und (2) in Abb. 2).

Kette Gibt es einen geschlossenen Pfad im Stromkreis? Der Stromkreis kann durch beliebige Zweige geschlossen werden, einschließlich bedingter Zweige, deren Widerstand gleich unendlich ist.

In Abb. 3 zeigt einen verzweigten Stromkreis, der aus drei Zweigen besteht.

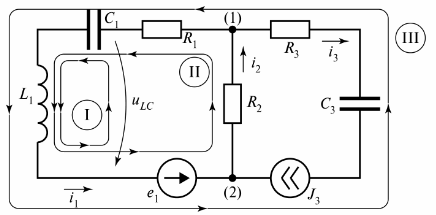
Reis. 3. Stromkreis mit zwei Stromkreisen

Das Diagramm zeigt drei Stromkreise, und Stromkreis I ist durch einen Zweig mit unendlichem Widerstand geschlossen. Dieser Zweig wird als Spannung tiLC bezeichnet.

Für die Schaltung von Abb. 3 ist es möglich, viele Schleifen zu bilden, die durch reale oder bedingte Zweige geschlossen werden, aber für die Berechnung des elektrischen Rauschens wird das Konzept der „unabhängigen Schleife“ verwendet. Die Anzahl der unabhängigen Kreisschleifen wird immer als das für die Berechnung erforderliche Minimum festgelegt.

Unabhängige Stromkreise sind immer geschlossen, aber Zweige, deren Widerstand ungleich unendlich ist, und jeder unabhängige Stromkreis enthält mindestens einen Zweig, der nicht in anderen Stromkreisen enthalten ist. Bei komplexen Stromkreisen können Sie anhand des Schaltplans die Anzahl der unabhängigen Stromkreise ermitteln.

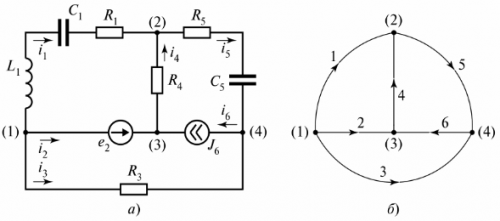
Auf dem Schaltplan Man nennt eine bedingte Darstellung der Schaltung, bei der jeder Zweig durch ein Liniensegment ersetzt wird. Artikel in Filialen werden nicht angezeigt. In FIG. 4 zeigt einen Zweigstromkreis und sein Diagramm.

Reis. 4. Verzweigter Stromkreis: a – Schaltplan, b – Diagramm

Um ein Diagramm aus einem Diagramm zu erstellen, müssen Sie die Knoten mit Zweiglinien verbinden, ohne Elemente darauf anzugeben. Die Zweige sind nummeriert und die Richtung der Ströme auf ihnen ist durch Pfeile angegeben. Der Graph selbst hat keine physikalische Bedeutung, kann aber zur Bestimmung der Anzahl und Art der unabhängigen Konturen verwendet werden. Zu diesem Zweck wird ein „grafischer Baum“ erstellt.

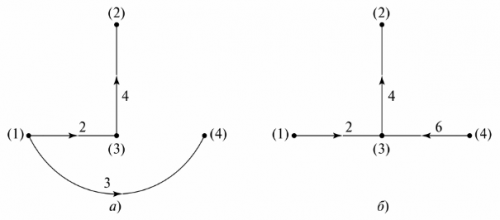
Grafischer Baum Es stellt den Graphen eines Stromkreises dar, dessen Knoten durch Verzweigungen so verbunden sind, dass kein geschlossener Regelkreis entsteht. Es gibt möglicherweise mehrere Möglichkeiten, einen grafischen Baum anzuzeigen. In Abb. 5 zeigt zwei mögliche Optionen für die Schaltung von FIG. 4.

Reis. 5. Grafischer Baum des Schemas

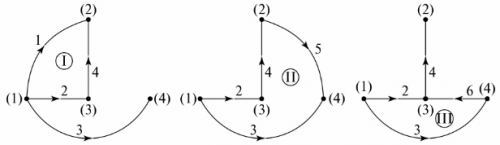
Die Anzahl der fehlenden Zweige im Diagrammbaum ist gleich der Anzahl der unabhängigen Schleifen der Schaltung. Im Beispiel sind dies drei Zweige, drei unabhängige Schleifen. Die Konfiguration unabhängiger Schleifen kann durch sequentielles Verbinden der Knoten des Diagrammbaums mit Zweigen erreicht werden, die nicht im Diagrammbaum angegeben sind. Zum Beispiel für den Diagrammbaum in Abb. 5, und die unabhängigen Konturen sind in Abb. dargestellt. 6.

Reis. 6. Bestimmen unabhängiger Konturen durch den Diagrammbaum

Die Auswahl einer Option zur Konfiguration unabhängiger Schaltkreise zur Berechnung des Schaltkreises erfolgt bei der Schaltkreisanalyse. Solche Konturen sollten Sie so wählen, dass die Berechnung möglichst einfach ist, d.h. die Anzahl der abhängigen Gleichungen im System ist minimal.

Topologische Gleichungen stellen eine Beziehung zwischen Spannungen und Strömen in einem Stromkreis her, und die Anzahl und Art der Gleichungen hängt nicht davon ab, welche Elemente in den Zweigen enthalten sind. Topologische Gleichungen umfassen Gleichungen, die bestehen aus nach Kirchhoffs Gesetzen.