Dreiphasige Netzversorgung: aktiv, reaktiv, voll

Die Werte der gesamten Wirk- und Gesamtblindleistung des Drehstromkreises sind gleich den Summen der Wirk- und Blindleistung für jede der drei Phasen A, B und C. Diese Aussage wird durch Folgendes veranschaulicht Formeln:

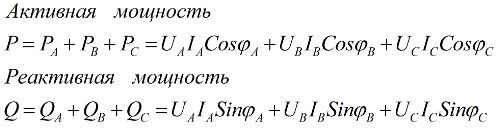
Dabei sind Ua, Ub, Uc, Ia, Ib, Ic die Werte der Phasenspannungen und -ströme und φ die Phasenverschiebung.

Wenn die Last symmetrisch ist, d. h. unter Bedingungen, bei denen die Wirk- und Blindleistung jeder Phase einander gleich sind, reicht es aus, den Wert der Phasenleistung mit zu multiplizieren, um die Gesamtleistung des Mehrphasenkreises zu ermitteln die Anzahl der beteiligten Phasen. Die Gesamtleistung wird anhand der erhaltenen Werte ihrer Wirk- und Blindkomponenten bestimmt:

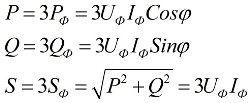
In den obigen Formeln können die Phasenwerte der Größen durch ihre linearen Werte ausgedrückt werden, die für Benutzer bei Stern- oder Dreieck-Verbindungsschemata unterschiedlich sein werden, aber die Leistungsformeln werden letztendlich dieselben sein:

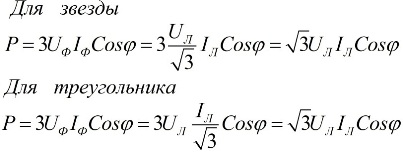
Aus den obigen Ausdrücken folgt, dass unabhängig vom Anschlussschema der Empfänger elektrischer Energie, sei es ein Dreieck oder ein Stern, wenn die Last symmetrisch ist, die Formeln zur Ermittlung der Leistung die gleiche Form haben, sowohl für a Dreieck und für einen Stern:

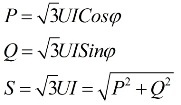
Diese Formeln zeigen lineare Werte von Spannung und Strom und werden ohne Indizes geschrieben. Normalerweise findet man eine solche Notation ohne Indizes, das heißt, wenn es keine Indizes gibt, dann meinen wir lineare Werte.

Ein spezielles Messgerät, genannt Wattmeter… Seine Messwerte werden durch die Formel bestimmt:

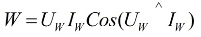
In der obigen Formel sind Uw und Iw die Vektoren der an der Last anliegenden Spannung und des durch sie fließenden Stroms.

Die Art der aktiven Last und das Phasenanschlussdiagramm können unterschiedlich sein. Daher sind die Anschlussdiagramme des Wattmeters je nach den jeweiligen Umständen unterschiedlich.

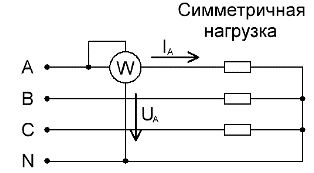
Bei symmetrisch belasteten Drehstromkreisen reicht für eine grobe Messung der gesamten Wirkleistung, wenn keine hohe Genauigkeit erforderlich ist, ein Wattmeter aus, das nur an eine der Phasen angeschlossen ist. Um den Wert der Wirkleistung des gesamten Stromkreises zu erhalten, müssen anschließend die Messwerte des Wattmeters mit der Anzahl der Phasen multipliziert werden:

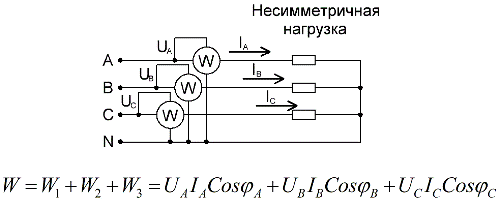
Für einen Vierleiterstromkreis mit Neutralleiter sind zur genauen Messung der Wirkleistung drei Wattmeter erforderlich, die jeweils abgelesen und dann summiert werden, um einen Wert für die Gesamtleistung des Stromkreises zu erhalten:

Wenn in einem Drehstromkreis kein Neutralleiter vorhanden ist, reichen zwei Wattmeter aus, um die Gesamtleistung zu messen, auch bei unsymmetrischer Belastung.

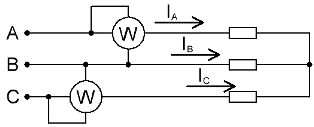
In Abwesenheit eines Neutralleiters sind die Phasenströme nach dem ersten Kirchhoffschen Gesetz miteinander verbunden:

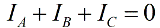
Dann ist die Summe der Messwerte eines Wattmeterpaares gleich:

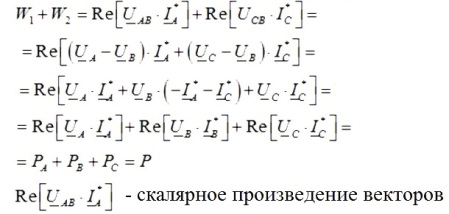
Wenn Sie also die Messwerte eines Wattmeterpaars addieren, erhalten Sie die gesamte Wirkleistung im untersuchten dreiphasigen Stromkreis, und die Messwerte der Wattmeter hängen sowohl von der Größe der Last als auch von ihrer Art ab.

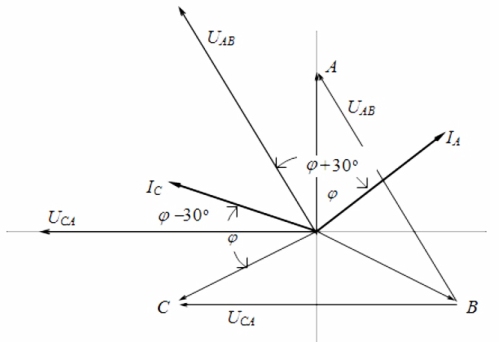
Betrachtet man das Vektordiagramm von Strömen und Spannungen im Zusammenhang mit einer symmetrischen Last, kann man schließen, dass die Messwerte von Wattmetern durch die folgenden Formeln bestimmt werden:

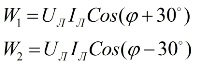
Nach der Analyse dieser Ausdrücke kann man verstehen, dass bei einer rein aktiven Last, wenn φ = 0, die Messwerte der beiden Wattmeter einander gleich sind, d. h. W1 = W2.

Bei aktiver Lastinduktivität, wenn 0 ≤ φ ≤ 90 °, sind die Messwerte von Wattmeter 1 kleiner als die von Wattmeter 2, d. h. W1 60 °, die Messwerte von Wattmeter 1 sind negativ, d. h. W1 <0.

Bei aktiv-kapazitiver Natur der Last sind die Messwerte des Wattmeters 2 kleiner als die des Wattmeters 1, wenn 0 ≥ φ≥ -90 °, d. h. W1 > W2. Bei φ <-60° werden die Messwerte des Wattmeters 2 negativ.