Grundparameter des Wechselstroms: Periode, Frequenz, Phase, Amplitude, harmonische Schwingungen

Wechselstrom ist ein elektrischer Strom, dessen Richtung und Stärke sich periodisch ändert. Da die Stärke des Wechselstroms normalerweise nach einem Sinusgesetz variiert, handelt es sich bei Wechselstrom um sinusförmige Schwankungen von Spannung und Strom.

Daher gilt alles, was für sinusförmige elektrische Schwingungen gilt, auch für Wechselstrom. Sinusförmige Schwingungen sind Schwingungen, bei denen sich der Schwingwert gemäß dem Sinusgesetz ändert. In diesem Artikel werden wir über Wechselstromparameter sprechen.

Die Änderung der EMF und die Änderung des Stroms einer linearen Last, die an eine solche Quelle angeschlossen ist, folgen einem Sinusgesetz. In diesem Fall können Wechsel-EMF, Wechselspannungen und -ströme durch ihre vier Hauptparameter charakterisiert werden:

• Zeitraum;

• Frequenz;

• Amplitude;

• effektiver Wert.

Es gibt auch zusätzliche Parameter:

• Winkelfrequenz;

• Phase;

• unmittelbarer Wert.

Als nächstes werden wir alle diese Parameter einzeln und zusammen betrachten.

Periode T.

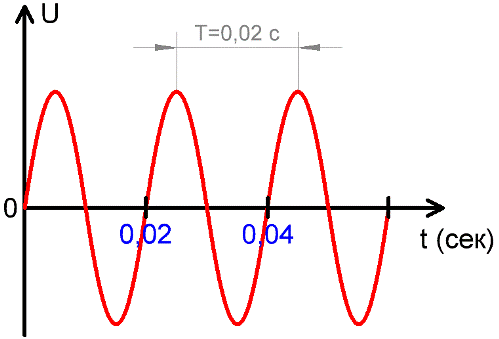
Periode – die Zeit, die ein oszillierendes System benötigt, um alle Zwischenzustände zu durchlaufen und wieder in seinen Ausgangszustand zurückzukehren.

Die Periode T eines Wechselstroms ist das Zeitintervall, in dem der Strom oder die Spannung einen vollständigen Änderungszyklus durchführt.

Da die Wechselstromquelle ein Generator ist, hängt die Periode von der Drehzahl seines Rotors ab. Je höher die Drehzahl der Wicklung oder des Rotors des Generators ist, desto kürzer ist die Periode der erzeugten Wechsel-EMF und dementsprechend ergibt sich der Wechselstrom der Last.

Der Zeitraum wird in Sekunden, Millisekunden, Mikrosekunden, Nanosekunden gemessen, abhängig von der jeweiligen Situation, in der dieser Strom betrachtet wird. Die obige Abbildung zeigt, wie sich die Spannung U über die Zeit bei konstanter Kennperiode T ändert.

Häufigkeit f

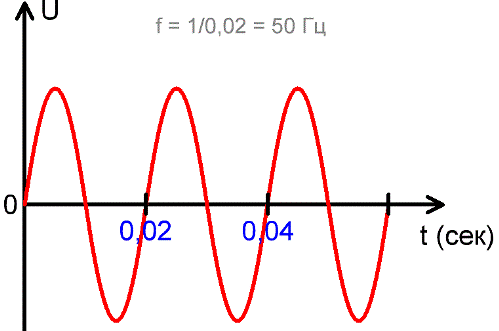
Die Frequenz f ist der Kehrwert der Periode und entspricht numerisch der Anzahl der Perioden der Strom- oder EMF-Änderung in 1 Sekunde. Das heißt, f = 1 / T. Die Maßeinheit der Frequenz ist Hertz (Hz), benannt nach dem deutschen Physiker Heinrich Hertz, der im 19. Jahrhundert maßgeblich zur Entwicklung der Elektrodynamik beigetragen hat. Je kürzer der Zeitraum, desto höher ist die Frequenz der EMF oder Stromänderung.

Heute beträgt in Russland die Standardfrequenz des Wechselstroms in Stromnetzen 50 Hz, d. h. in 1 Sekunde treten 50 Schwankungen der Netzspannung auf.

In anderen Bereichen der Elektrodynamik werden höhere Frequenzen verwendet, beispielsweise 20 kHz und mehr bei modernen Wechselrichtern, in engeren Bereichen der Elektrodynamik bis zu mehreren MHz. In der obigen Abbildung können Sie sehen, dass es in einer Sekunde 50 vollständige Schwingungen gibt, die jeweils 0,02 Sekunden dauern und 1 / 0,02 = 50.

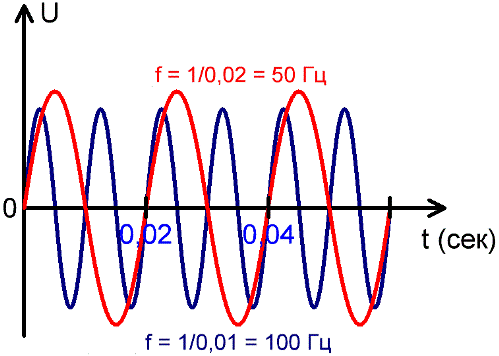
Aus den Diagrammen der zeitlichen Änderung des sinusförmigen Wechselstroms ist ersichtlich, dass Ströme unterschiedlicher Frequenz im gleichen Zeitintervall eine unterschiedliche Anzahl von Perioden enthalten.

Winkelfrequenz

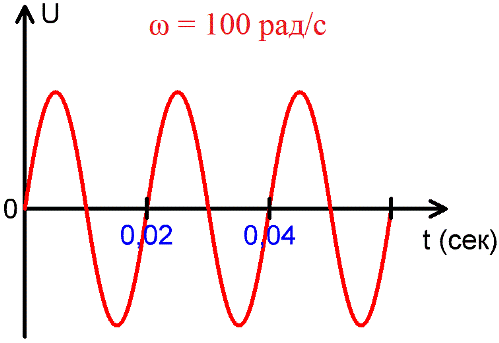
Winkelfrequenz – die Anzahl der Schwingungen, die in 2pi Sek. erzeugt werden.

In einer Periode ändert sich die Phase der sinusförmigen EMK oder des sinusförmigen Stroms um 2 pi im Bogenmaß oder 360 °, daher ist die Kreisfrequenz des sinusförmigen Wechselstroms gleich:

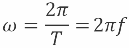
Verwenden Sie die Anzahl der Schwingungen in 2pi Sek. (nicht in 1 Sek.). Dies ist praktisch, da in den Formeln das Gesetz der Spannungs- und Stromänderung bei harmonischen Schwingungen ausgedrückt wird, der induktive oder kapazitive Widerstand von Wechselstrom usw. ausgedrückt wird In anderen Fällen erscheint die Schwingungsfrequenz n zusammen mit dem Multiplikator 2pi.

Phase

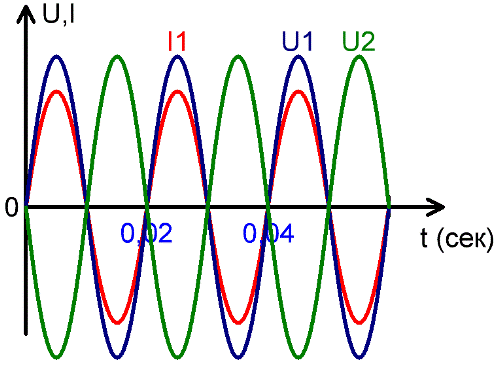
Phase – Zustand, Phase eines periodischen Prozesses. Bei Sinusschwingungen hat der Begriff Phase eine eindeutigere Bedeutung. In der Praxis spielt meist nicht die Phase selbst eine Rolle, sondern die Phasenverschiebung zwischen zwei beliebigen periodischen Prozessen.

In diesem Fall wird unter dem Begriff „Phase“ ein Entwicklungsstadium des Prozesses verstanden, und in diesem Fall wird die Phase in Bezug auf Wechselströme und Sinusspannungen als Zustand des Wechselstroms zu einem bestimmten Zeitpunkt bezeichnet Zeit.

Die Abbildungen zeigen: das Zusammentreffen von Spannung U1 und Strom I1 in Phase, Spannung U1 und U2 in Gegenphase sowie die Phasenverschiebung zwischen Strom I1 und Spannung U2. Die Phasenverschiebung wird im Bogenmaß, Teilen einer Periode, in Grad gemessen.

Siehe auch: Was ist Phase, Phasenwinkel und Phasenverschiebung?

Amplitude Ähm und ich

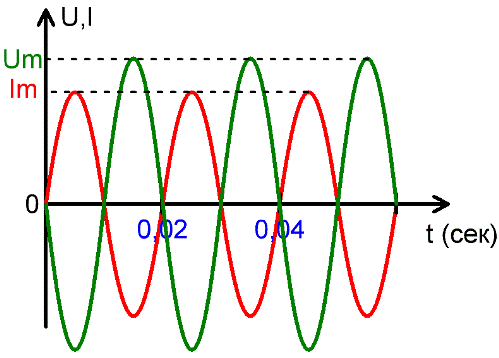
Wenn man von der Größe eines sinusförmigen Wechselstroms oder einer sinusförmigen Wechsel-EMF spricht, wird der höchste Wert der EMF oder des Stroms als Amplitude oder Amplitudenwert (Maximum) bezeichnet.

Amplitude — der größte Wert der Größe, die harmonische Schwingungen ausführt (z. B. der Maximalwert der Stromstärke im Wechselstrom, die Abweichung des oszillierenden Pendels von der Gleichgewichtslage), die größte Abweichung der oszillierenden Größe von einem bestimmten Wert, bedingt als Anfangsnullpunkt akzeptiert.

Der Begriff Amplitude bezieht sich streng genommen nur auf Sinusschwingungen, wird aber meist (nicht ganz korrekt) im obigen Sinne auf alle Schwingungen angewendet.

Wenn wir von einem Wechselstromgenerator sprechen, erreicht die EMF seiner Anschlüsse zweimal pro Periode einen Amplitudenwert, von dem der erste während der positiven und negativen Halbzyklen + Em und der zweite Em ist. Das aktuelle I verhält sich ähnlich und wird entsprechend mit Im bezeichnet.

Harmonische Schwingungen – Schwingungen, bei denen sich eine oszillierende Größe, beispielsweise die Spannung in einem Stromkreis, mit der Zeit gemäß einem harmonischen Sinus- oder Kosinusgesetz ändert. Grafisch dargestellt durch eine Sinuskurve.

Reale Prozesse können harmonische Schwingungen nur annähern. Wenn die Schwingungen jedoch die charakteristischsten Merkmale des Prozesses widerspiegeln, gilt ein solcher Prozess als harmonisch, was die Lösung vieler physikalischer und technischer Probleme erheblich erleichtert.

Bewegungen, die harmonischen Schwingungen ähneln, treten in verschiedenen Systemen auf: mechanisch (Schwingungen eines Pendels), akustisch (Schwingungen einer Luftsäule in einer Orgelpfeife), elektromagnetisch (Schwingungen in einem LC-Kreis) usw.Die Schwingungstheorie betrachtet diese physikalisch unterschiedlichen Phänomene aus einem einheitlichen Blickwinkel und bestimmt ihre gemeinsamen Eigenschaften.

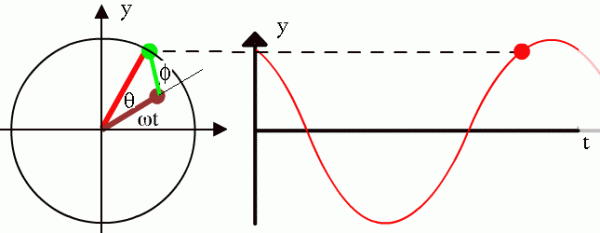
Es ist praktisch, harmonische Schwingungen grafisch darzustellen, indem man einen Vektor verwendet, der sich mit konstanter Winkelgeschwindigkeit um eine Achse senkrecht zu diesem Vektor dreht und durch seinen Ursprung verläuft. Die Drehwinkelgeschwindigkeit des Vektors entspricht der Kreisfrequenz der harmonischen Schwingung.

Vektordiagramm einer harmonischen Schwingung

Ein periodischer Prozess beliebiger Form kann in eine unendliche Reihe einfacher harmonischer Schwingungen mit unterschiedlichen Frequenzen, Amplituden und Phasen zerlegt werden.

Harmonisch – eine harmonische Schwingung, deren Frequenz um ein Vielfaches größer ist als die Frequenz einer anderen Schwingung, die als Grundton bezeichnet wird. Die Zahl der Harmonischen gibt an, wie oft ihre Frequenz größer ist als die Frequenz des Grundtons (z. B. ist die dritte Harmonische eine harmonische Schwingung mit einer Frequenz, die dreimal höher ist als die Frequenz des Grundtons).

Alle periodischen, aber nicht harmonischen (d. h. von der Sinusform abweichenden) Schwingungen können als Summe harmonischer Schwingungen dargestellt werden – dem Grundton und einer Reihe von Harmonischen. Je mehr sich die betrachtete Schwingung in ihrer Form von einer Sinusschwingung unterscheidet, desto mehr Harmonische enthält sie.

Momentanwert von u und i

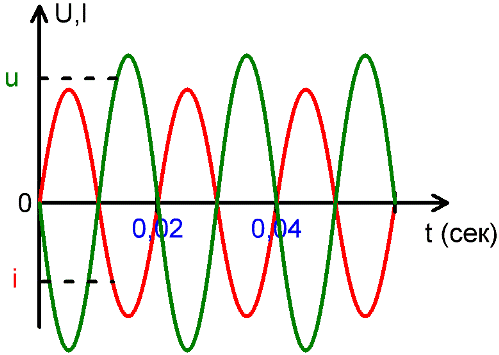
Der Wert der EMK oder des Stroms zu einem bestimmten Zeitpunkt wird als Momentanwert bezeichnet und mit den Kleinbuchstaben u und i bezeichnet. Da sich diese Werte jedoch ständig ändern, ist es unpraktisch, daraus die Wechselströme und EMFs abzuschätzen.

RMS-Werte von I, E und U

Die Fähigkeit von Wechselstrom, nützliche Arbeit zu verrichten, beispielsweise den Rotor eines Motors mechanisch zu drehen oder Wärme an einem Heizgerät zu erzeugen, lässt sich bequem anhand der Effektivwerte von EMK und Strömen abschätzen.

So, effektiver Barwert nennt man den Wert eines solchen Gleichstroms, der beim Durchgang durch einen Leiter während einer Periode des betrachteten Wechselstroms die gleiche mechanische Arbeit bzw. die gleiche Wärmemenge wie dieser Wechselstrom erzeugt.

Die Effektivwerte von Spannungen, EMKs und Strömen werden durch die Großbuchstaben I, E und U angegeben. Für sinusförmigen Wechselstrom und für sinusförmige Wechselspannung sind die Effektivwerte:

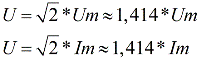
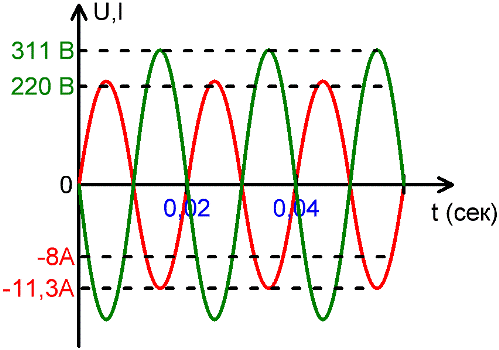
Zur Beschreibung elektrischer Netze ist es sinnvoll, den Effektivwert von Strom und Spannung zu verwenden. Beispielsweise ist ein Wert von 220–240 Volt der Effektivwert der Spannung in modernen Haushaltssteckdosen, und die Amplitude ist viel höher – von 311 bis 339 Volt.

Das Gleiche gilt für den Strom. Wenn beispielsweise gesagt wird, dass durch ein Haushaltsheizgerät ein Strom von 8 Ampere fließt, ist damit ein Effektivwert gemeint, während die Amplitude 11,3 Ampere beträgt.

Auf die eine oder andere Weise sind mechanische Arbeit und elektrische Energie in elektrischen Anlagen proportional zu den Effektivwerten von Spannungen und Strömen. Ein erheblicher Teil der Messgeräte zeigt exakt die Effektivwerte von Spannungen und Strömen an.