Stromkreise mit nicht sinusförmigem Strom

Nichtsinusförmige Ströme und ihre Zerlegung

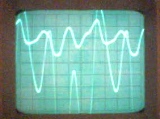In einem Stromkreis können nicht-sinusförmige Ströme aus zwei Gründen auftreten:

1. Der Stromkreis selbst ist linear, aber auf den Stromkreis wirkt eine nichtsinusförmige Spannung.

2. Die auf den Stromkreis wirkende Spannung ist sinusförmig, der Stromkreis enthält jedoch nichtlineare Elemente.

Es kann beide Gründe geben. In diesem Kapitel geht es nur um Schaltungen für den ersten Punkt. In diesem Fall werden die nichtsinusförmigen Spannungen als periodisch betrachtet.

Generatoren periodischer Impulse werden in verschiedenen Geräten der Funktechnik, Automatisierung und Telemechanik eingesetzt. Die Form der Impulse kann unterschiedlich sein: Säge, gestuft, rechteckig (Abb. 1).

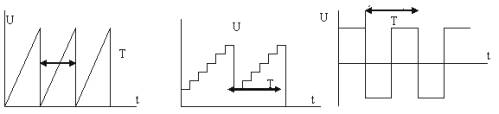
Abbildung 1. Pulsformen

Die Phänomene, die in einem linearen Stromkreis unter periodischen, aber nicht sinusförmigen Spannungen auftreten, lassen sich am einfachsten untersuchen, wenn die Spannungskurve in einer trigonometrischen Fourier-Reihe entwickelt wird:

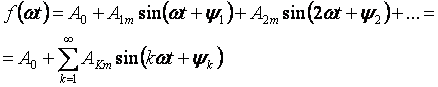
Der erste Term der Reihe A0 wird als konstante Komponente oder nullte Harmonische bezeichnet, der zweite Term der Reihe

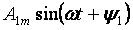
– die Grund- oder erste Harmonische und alle anderen Mitglieder der Form

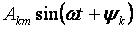
für k>1 werden höhere Harmonische genannt.

Wenn wir im Ausdruck (3.1) den Sinus der Summe öffnen, können wir zu einer anderen Schreibweise der Reihe übergehen:

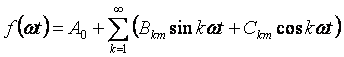Wenn die Funktion symmetrisch zur Abszissenachse ist, enthält die Reihe keine konstante Komponente. Wenn die Funktion symmetrisch zur Ordinatenachse ist, enthält die Reihe keine Sinuswerte. Die Funktion ist symmetrisch zum Ursprung und enthält keine Kosinuswerte.

Einige Beispiele für Serienerweiterungen sind in einer Tabelle aufgeführt. 1 und sind auch in der Referenzliteratur verfügbar.

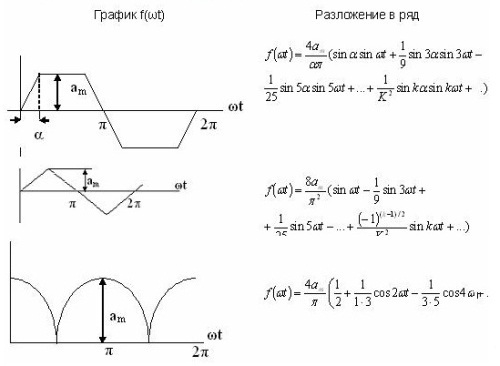
Tabelle 1. Fourier-Reihenentwicklung

Berechnung nichtsinusförmiger Stromkreise

Die Schaltung wird für jede Harmonische nach dem Modell berechnet. Der Stromkreis wird so oft berechnet, wie Harmonische in der auf den Stromkreis wirkenden Spannung vorhanden sind. In diesem Fall müssen eine Reihe von Merkmalen berücksichtigt werden.

Es ist zu beachten, dass der Widerstand des induktiven Elements mit zunehmender Harmonischenzahl zunimmt

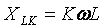
und das kapazitive Element nimmt im Gegenteil ab:

Es ist auch zu berücksichtigen, dass der konstante Anteil des Stroms nicht durch den Kondensator fließt und die Induktivität kein Widerstand dafür ist.

Darüber hinaus sollte man die möglichen Resonanzerscheinungen nicht nur bei der Grundschwingung, sondern auch bei höheren Harmonischen nicht außer Acht lassen.

Vektordiagramme kann für jede Harmonische separat dargestellt werden.

Nach dem Superpositionsprinzip kann der Strom jedes Zweigs aus der Summe einzelner Terme (Null-, Grund- und höhere Harmonische) bestehen:

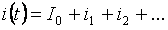
Der Effektivwert des gesamten Zweigstroms lässt sich aus dem Mittelwert der einzelnen Oberschwingungsströme ermitteln:

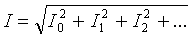
Die Wirkleistung des nichtsinusförmigen Stroms ist gleich der Summe der Wirkleistungen der einzelnen Harmonischen:

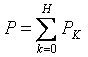
Nachfolgend finden Sie ein allgemeines Beispiel zur Berechnung nichtsinusförmiger Stromkreise. Alle Ströme, Spannungen und Widerstände haben zwei Indizes: Die erste Ziffer bedeutet die Zweignummer und die zweite Ziffer die harmonische Zahl. Eingangsspannung:

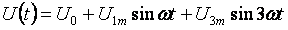
• Permanenter Bestandteil

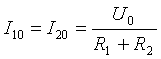
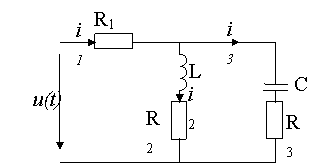
Abbildung 2. Elektrischer Schaltplan

• Dur-Harmonische:

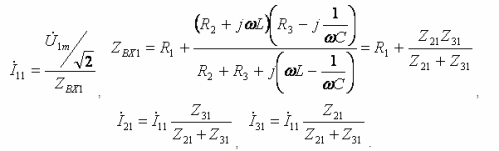
• Dritte Harmonische:

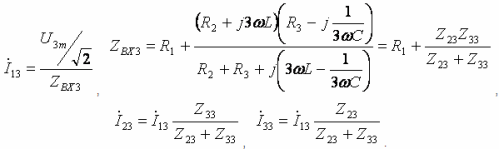
Lesen Sie auch: Die gebräuchlichsten AC-zu-DC-Gleichrichtungsschemata