Berechnungen zur Verbesserung des Leistungsfaktors in einem Drehstromnetz
Bei der Berechnung der Kapazität eines Kondensators zur Verbesserung des Leistungsfaktors in einem Drehstromnetz halten wir uns an die gleiche Reihenfolge wie im Artikel mit Beispielen für Berechnungen in einem einphasigen Netzwerk… Der Wert des Leistungsfaktors wird durch die Leistungsformel für Drehstrom bestimmt:
P1 = √3 ∙ U ∙ I ∙ cosφ, cosφ = P1 / (√3 ∙ U ∙ I).
Beispiele von
1. Ein Drehstrom-Induktionsmotor hat folgende Paneldaten: P = 40 kW, U = 380 V, I = 105 A, η = 0,85, f = 50 Hz. Sternschaltung des Stators. Angenommen, es ist schwierig, den cosφ-Wert der Platine zu bestimmen, und daher ist es notwendig, ihn zu bestimmen. Auf welchen Wert sinkt der Strom, nachdem der Leistungsfaktor mithilfe von Kondensatoren auf cosφ = 1 verbessert wurde? Welche Kapazität sollten die Kondensatoren haben? Welche Blindleistung kompensieren die Kondensatoren (Abb. 1)?
Die Klemmen der Statorwicklung sind gekennzeichnet: Anfang – C1, C2, C3, Enden – C4, C5, C6.Um die Kommunikation mit den Diagrammen zu erleichtern, wird im Folgenden jedoch der Ursprung mit A, B, C und die Enden mit X, Y, Z bezeichnet.
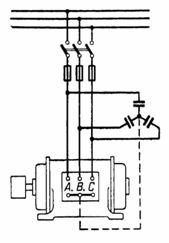
Reis. 1.
Motorleistung P1 = P2 / η = 40000 / 0,85 ≈47000 W,
Dabei ist P2 die auf dem Typenschild des Motors angegebene Nettoleistung.
cosφ = P1 / (√3 ∙ U ∙ I) = 47000 / (√3 ∙ 380 ∙ 105) = 0,69.
Nach der Verbesserung des Leistungsfaktors auf cosφ = 1 beträgt die Eingangsleistung:
P1 = √3 ∙ U ∙ I ∙ 1
und der Strom sinkt auf
I1 = P1 / (√3 ∙ U) = 47000 / (1,73 ∙ 380) = 71,5 A.
Dies ist der Wirkstrom bei cosφ = 0,69 seit
Ia = I ∙ cosφ = 105 ∙ 0,69 = 71,5 A.
In Abb. 1 zeigt die Einbeziehung von Kondensatoren zur Verbesserung des cosφ.
Kondensatorspannung Uph = U / √3 = 380 / √3 = 220 V.
Der Phasenmagnetisierungsstrom ist gleich dem linearen Magnetisierungsstrom: IL = I ∙ sinφ = 105 ∙ 0,75 = 79,8 A.
Der kapazitive Widerstand des Kondensators, der den Magnetisierungsstrom bereitstellen muss, beträgt: xC = Uph / IL = 1 / (2 ∙ π ∙ f ∙ C).
Daher beträgt die Kapazität des Kondensators C = IC / (Uph ∙ 2 ∙ π ∙ f) = 79,8 / (220 ∙ 3,14 ∙ 100) = 79,800 / (22 ∙ 3,14) ∙ 10 ^ (- 6) = 1156,4 μF.
An einen Drehstrommotor muss ein Kondensatorblock mit einer Gesamtkapazität von C = 3 ∙ 1156,4≈3469 μF angeschlossen werden, um den Leistungsfaktor auf cosφ = 1 zu verbessern und gleichzeitig den Strom von 105 auf 71,5 A zu reduzieren.
Die gesamte durch Kondensatoren kompensierte Blindleistung, die bei Fehlen von Kondensatoren dem Netz entnommen wird, beträgt Q = 3 ∙ Uph ∙ IL = 3 ∙ 220 ∙ 79,8≈52668 = 52,66 kvar.
In diesem Fall bezieht der Motor Wirkleistung P1 = 47 kW nur aus dem Netz.
In Abb.2 zeigt einen Block von Kondensatoren, die im Dreieck geschaltet sind und an die Klemmen eines Drehstrommotors angeschlossen sind, dessen Wicklung ebenfalls im Dreieck geschaltet ist. Diese Verbindung von Kondensatoren ist vorteilhafter als die in Abb. gezeigte Verbindung. 1 (siehe Fazit der Berechnung 2).
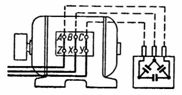
Reis. 2.
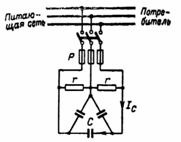
2. Ein Kleinkraftwerk speist ein Drehstromnetz mit einem Strom I = 250 A bei einer Netzspannung U = 380 V und einem Netzleistungsfaktor cosφ = 0,8. Die Verbesserung des Leistungsfaktors wird durch Kondensatoren erreicht, die gemäß dem Diagramm in Abb. in Dreieck geschaltet sind. 3. Es ist notwendig, den Wert der Kapazität der Kondensatoren und der kompensierten Blindleistung zu bestimmen.
Reis. 3.
Scheinleistung S = √3 ∙ U ∙ I = 1,73 ∙ 380 ∙ 250 = 164,3 kVA.
Bestimmen Sie die Wirkleistung bei cosφ = 0,8:
P1 = √3 ∙ U ∙ I ∙ cosφ = S ∙ cosφ≈164,3 ∙ 0,8 = 131,5 W.
Zu kompensierende Blindleistung bei cosφ = 0,8
Q = S ∙ sinφ≈164,3 ∙ 0,6 = 98,6 kvar.
Daher ist der lineare Magnetisierungsstrom (Abb. 3) IL = I ∙ sinφ = Q / (√3 ∙ U) ≈150 A.
Magnetisierender (kapazitiver) Phasenstrom ICph = Q / (3 ∙ U) = 98580 / (3 ∙ 380) = 86,5 A.
Der Kondensatorstrom kann auf andere Weise durch den Magnetisierungsstrom (Blindstrom) im Stromkreis bestimmt werden:
IL = I ∙ sinφ = 250 ∙ 0,6 = 150 A,
ICph = ILph = IL / √3 = 150 / 1,73 = 86,7 A.
Bei Dreieckschaltung hat jede Kondensatorgruppe eine Spannung von 380 V und einen Phasenstrom ICph = 86,7 A.
I = ICf = U / xC = U / (1⁄ (ω ∙ C)) = U ∙ ω ∙ C.
Daher ist C = IC / (U ∙ 2 ∙ π ∙ f) = 86,7 / (300 ∙ π ∙ 100) = 726 μF.
Die Gesamtkapazität der Kondensatorbank beträgt C3 = 3 ∙ 726 = 2178 μF.
Durch die angeschlossenen Kondensatoren ist es möglich, die gesamte Leistung des Kraftwerks S = 164,3 kVA in Form von Nettoleistung zu nutzen.Ohne Betriebskondensatoren wird bei cosφ = 0,8 nur eine Wirkleistung von 131,5 kW genutzt.
Die kompensierte Blindleistung Q = 3 ∙ U ∙ IC = 3 ∙ ω ∙ C ∙ U ^ 2 steigt proportional zum Quadrat der Spannung. Daher sind die erforderliche Kapazität der Kondensatoren und damit die Kosten der Kondensatoren geringer, da die Spannung höher ist.
Widerstände r in Abb. 3 dienen zur allmählichen Entladung von Kondensatoren, wenn diese vom Netz getrennt werden.