Berechnung der Kondensatorkapazität
Die Kapazität C ist die Kapazität des Kondensators, die Strommenge Q in Amperesekunden oder die Ladung Q in Amperesekunden aufzunehmen (zu speichern und zu halten). Sagt man einem Körper, zum Beispiel einer Kugel, eine elektrische Ladung (Strommenge) Q, so zeigt ein zwischen diesem Körper und der Erde angeschlossenes Elektroskop eine Spannung U an (Abb. 1). Diese Spannung ist proportional zur Ladung und hängt auch von der Form und Größe des Körpers ab.
Der Zusammenhang zwischen Ladung Q und Spannung U wird durch die Formel Q = C ∙ U ausgedrückt.
Die Proportionalitätskonstante C wird Kapazität des Körpers genannt. Wenn der Körper die Form einer Kugel hat, ist die Kapazität des Körpers proportional zum Radius der Kugel r.
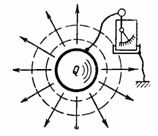
Reis. 1.
Die Maßeinheit für die Kapazität ist Farad (F).
Der Körper hat eine Kapazität von 1 F, wenn eine Ladung von 1 k eine Spannung von 1 V zwischen ihm und der Erde erzeugt. Farad ist eine sehr große Maßeinheit, daher werden in der Praxis kleinere Einheiten verwendet: Mikrofarad (μF), Nanofarad (nF) und Picofarad (pF)...
Diese Einheiten hängen durch die folgenden Verhältnisse zusammen: 1 Ф = 10 ^ 6 μF; 1 μF = 10 ^ 6 pF; 1 nF = 10 ^ 3 pF.
Die Kapazität einer Kugel mit einem Radius von 1 cm beträgt 1,1 pF.
Nicht nur ein isolierter Körper kann Ladung ansammeln, sondern auch ein spezielles Gerät namens Kondensator. Ein Kondensator besteht aus zwei oder mehr Platten (Platten), die durch ein Dielektrikum (Isolierung) getrennt sind.
In Abb. 2 zeigt eine Schaltung mit einer Gleichstromquelle, die an einen Kondensator angeschlossen ist. Beim Einschalten entsteht in der rechten Platte des Kondensators eine positive Ladung +Q und in der linken Platte eine negative Ladung –Q. Während Kondensatorladung Durch den Stromkreis fließt ein Strom, der nach dem Ende des Ladevorgangs stoppt. dann ist die Spannung am Kondensator gleich e. usw. c. Quelle U. Die Ladung auf der Kondensatorplatte, Spannung und Kapazität hängen durch das Verhältnis Q = C ∙ U zusammen. In diesem Fall bildet sich im Dielektrikum des Kondensators ein elektrostatisches Feld.
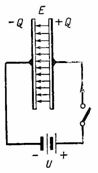
Reis. 2.
Die Kapazität eines Kondensators mit einem Luftdielektrikum kann nach der Formel C = S / (4 ∙ π ∙ d) ∙ 1,11, pF berechnet werden, wobei S die Fläche einer Platte, cm2 ist; d ist der Abstand zwischen den Platten, cm; C ist die Kapazität des Kondensators, pF.
Die Kapazität eines aus n Platten bestehenden Kondensators (Abb. 3) ist gleich: C = (n-1) ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.
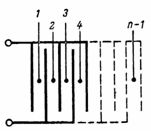
Reis. 3.
Wird der Raum zwischen den Platten mit einem anderen Dielektrikum, beispielsweise Papier, gefüllt, erhöht sich die Kapazität des Kondensators um den Faktor ε. Bei Verwendung von Papierisolierung erhöht sich die Kapazität um das Dreifache, bei Glimmerisolierung um das 5- bis 8-fache, bei Glas um das 7-fache usw. Der Wert von ε wird als Dielektrizitätskonstante des Dielektrikums bezeichnet.
Die allgemeine Formel zur Bestimmung der Kapazität eines Kondensators mit der Dielektrizitätskonstante ε (Epsilon) lautet: C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.
Diese Formel ist nützlich zur Berechnung kleiner variabler Kondensatoren für Radios.Die gleiche Formel kann wie folgt dargestellt werden: C = (ε_0 ∙ ε ∙ S) / d, wobei ε_0 die Dielektrizitätskonstante oder die Dielektrizitätskonstante des Vakuums ist (ε_0 = 8,859 ∙ 10 ^ (- 12) F / m); ε ist die Dielektrizitätskonstante des Dielektrikums.
In dieser Formel werden die Abmessungen in Metern ersetzt und die Kapazität in Farad erhalten.
Beispiele von
1. Welche Kapazität hat der Planet Erde, dessen Radius r = 6378 km beträgt?
Da die Kapazität einer Kugel mit einem Radius von 1 cm 1,11 pF beträgt, beträgt die Kapazität der Erde: C = 637,8 ∙ 10 ^ 6 ∙ 1,11 = 707,95 ∙ 10 ^ 6 pF = 708 μF. (Die Kapazität einer Kugel von der Größe unseres Planeten ist relativ gering. Kleine Elektrolytkondensatoren haben diese Kapazität.)
2. Bestimmen Sie die Kapazität eines Kondensators, der aus zwei Platten besteht, von denen jede eine Fläche S = 120 cm2 hat.
Die Platten sind durch eine Luftschicht mit einer Dicke von d = 0,5 cm getrennt, C = S / (4 ∙ π ∙ d) ∙ 1,11 = (120 ∙ 1,11) / (4 ∙ π ∙ 0,5) = 21,20 pF .. .
3. Bestimmen Sie die Kapazität des Kondensators mit den im vorherigen Beispiel angegebenen Daten, wenn der Raum zwischen den Platten mit Wachspapier mit einer Dielektrizitätskonstanten ε = 4, Glas (ε = 7), Elektrokarton (ε = 2) gefüllt ist. , Glimmer (ε = 8 ).
Ein Wachspapierkondensator hat eine Kapazität C = ε ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = 4 ∙ 21,2 = 84,8 pF.
Die Kapazität eines Glaskondensators beträgt C = 7 ∙ 21,2 = 148,4 pF.
Die Kapazität des Pappkondensators beträgt C = 2 ∙ 21,2 = 42,3 pF.
Die Kapazität des Glimmerkondensators beträgt C = 8 ∙ 21,2 = 169,6 pF.
4. Wie groß ist die Kapazität eines Luftdrehkondensators für einen Funkempfänger bestehend aus 20 Platten mit einer Fläche von 20 cm2, wenn der Plattenabstand 0,06 cm beträgt (Abb. 149)?
C = (n-1) ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = (20-1) ∙ (20 ∙ 1,11) / (4 ∙ π ∙ 0,06) = 559, 44 pF.
Der in Abb. gezeigte Kondensator3, besteht aus einzelnen einfachsten Kondensatoren mit zwei Platten, deren Anzahl gleich n-1 ist.
5. Ein Papierkondensator mit der Kapazität C = 2 μF besteht aus zwei Streifen Alufolie C und zwei Streifen eines Dielektrikums aus Wachspapier B mit der Dielektrizitätskonstante ε = 6. Die Dicke des Wachspapiers beträgt d = 0,1 mm. Die gefalteten Streifen werden aufgerollt, aus den Stahlplatten werden die Leitungen gefertigt. Bestimmen Sie die Länge des Kondensatorstahlbandes, wenn seine Breite 4 cm beträgt (Abb. 4).
Reis. 4.
Zuerst bestimmen wir die Fläche eines Streifens durch die Formel C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, woraus S = (C ∙ 4 ∙ π ∙ d) / (ε ∙ 1,11) = ( 2 ∙ 4 ∙ π ∙ 0,01 ∙ 10 ^ 6) / (6 ∙ 1,11); S = 2.000.000 / (6 ∙ 1,11) ∙ 4 ∙ π ∙ 0,01 = 37680 cm2.
Die Länge jedes Streifens beträgt l = 37680/4 = 9420 cm = 94,2 m.