Berechnung des resultierenden Widerstandes bei Reihen-Parallelschaltung
Konzepte und Formeln
Eine Reihen-Parallel- oder Mischschaltung ist eine komplexe Verbindung von drei oder mehr Widerständen. Der resultierende Widerstand einer Mischschaltung wird stufenweise anhand von Formeln zur Berechnung von Widerständen in Reihen- und Parallelschaltungen berechnet.
Beispiele von
1. Berechnen Sie die Reihen-Parallelschaltung von drei Widerständen gemäß dem Diagramm in Abb. 1.
Ersetzen Sie zunächst die parallel geschalteten Widerstände r2 und r3 durch den resultierenden Widerstand r (2-3):
r (2-3) = (r2 ∙ r3) / (r2 + r3) = (10 ∙ 20) / 30 = 6,6 Ohm.
Der resultierende Widerstand des gesamten Stromkreises beträgt r = r1 + r (2-3) = 5 + 6,6 = 11,6 Ohm.
Reis. 1.
2. Welcher Strom fließt im offenen und geschlossenen Gehäuse durch den Stromkreis (Abb. 2). Messer wechseln P? Wie ändert sich in beiden Fällen die Spannung am Widerstand r2?
Reis. 2.
a) Der Schalter ist geöffnet. Resultierender Widerstand der in Reihe geschalteten Widerstände r1 und r2
r (1-2) = r1 + r2 = 25 Ohm.
Strom I (1-2) = U / r (1-2) = 100/25 = 4 A.
Spannungsabfall am Widerstand r2
U2 = I (1-2) ∙ r2 = 4 ∙ 5 = 20 V.
b) Der Schalter ist geschlossen. Resultierender Widerstand der parallel geschalteten Widerstände r1 und r3
r (1-3) = (r1 ∙ r3) / (r1 + r3) = (20 ∙ 10) / (20 + 10) = 200/30 = 6,6 Ohm.
Der Gesamtwiderstand des gesamten Stromkreises beträgt r = r (1-3) + r2 = 6,6 + 5 = 11,6 Ohm.
Strom I = U / r = 100 / 11,6 = 8,62 A.
Der Spannungsabfall am Widerstand r2 beträgt in diesem Fall: U2 = I ∙ r2 = 8,62 ∙ 5 = 43,25 V.
Im zweiten Fall erhöhte sich der Strom durch die Parallelschaltung des Widerstands R3. Mehr Strom schafft mehr Spannungsabfall am Widerstand r2.
3. Was sein sollte zusätzlicher Widerstand rd, so dass zwei parallel geschaltete Lampen für eine Spannung von 120 V und einen Strom von 0,2 A an ein Netz mit einer Spannung von U = 220 V angeschlossen werden können (Abb. 3)?
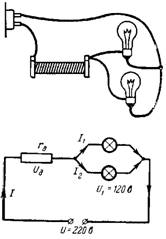
Reis. 3.
Die Spannung in den Lampen sollte 120 V betragen. Die verbleibende Spannung (100 V) fällt am Zusatzwiderstand rd an. Durch den Widerstand rd fließt ein Strom von zwei Lampen I = 0,4 A.
Nach dem Ohmschen Gesetz ist rd = Ud / I = 100 / 0,4 = 250 Ohm.
4. Elektronische Lampen mit einem 1,2-V-Glühfaden und einem Glühfadenstrom von 0,025 und 0,05 A werden in Reihe an eine Gleichstromquelle mit einer Spannung von 4,5 V geschaltet. Wie groß sollte der zusätzliche Widerstand rd und sein? Parallelwiderstand (Shunt) zu einer Lampe mit geringerem Wendelstrom (Abb. 4)?
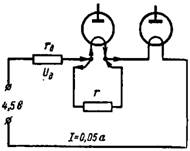
Reis. 4.
Die Widerstände im Stromkreis müssen so gewählt werden, dass der Glühstrom der zweiten Lampe I = 0,05 A fließt. Die Spannung an der Glühwendel der elektronischen Lampen beträgt 1,2 + 1,2 = 2,4 V. Subtrahiert man diesen Wert von der Batteriespannung, erhalten wir Nehmen Sie den Wert des Spannungsabfalls am Zusatzwiderstand rd: Ud = 4,5-2,4 = 2,1 V.
Daher beträgt der Zusatzwiderstand rd = (Ud) / I = 2,1 / 0,05 = 42 Ohm.
Durch den Glühfaden der ersten Vakuumröhre sollte kein Heizstrom von 0,05 A fließen. Die Hälfte dieses Stroms (0,05-0,025 = 0,025 A) muss durch den Shunt r fließen. Die Shunt-Spannung ist die gleiche wie die des Glühfadens der Lampe, d. h. 1,2 V. Daher beträgt der Shunt-Widerstand: r = 1,2 / 0,025 = 48 Ohm.
5. Wie hoch sind der resultierende Stromkreiswiderstand und der darin enthaltene Strom im Stromkreis von Abb. 5?
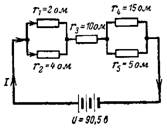
Reis. 5.
Bestimmen wir zunächst den resultierenden Widerstandswert der parallel geschalteten Widerstände:
r (1-2) = (r1 ∙ r2) / (r1 + r2) = (2 ∙ 4) / (2 + 4) = 8/6 = 1,3 Ohm;
r (4-5) = (r4 ∙ r5) / (r4 + r5) = (15 ∙ 5) / (15 + 5) = 75/20 = 3,75 Ohm.
Der resultierende Stromkreiswiderstand beträgt:
r = r (1-2) + r3 + r (4-5) = 1,3 + 10 + 3,75 = 15,05 Ohm.
Der resultierende Strom bei Spannung U = 90,5 V
I = U / r = 90,5 / 15,05 = 6 A.
6. Berechnen Sie den resultierenden Widerstand einer komplexen Reihen-Parallel-Verbindung in der Schaltung von Abb. 6. Berechnen Sie den resultierenden Strom I, den Strom I4 und den Spannungsabfall am Widerstand r1.
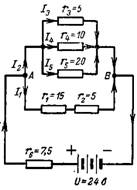
Reis. 6.
Resultierender Leitwert parallel geschalteter Widerstände
1 / r (3-4-5) = 1 / r3 + 1 / r4 + 1 / r5 = 1/5 + 1/10 + 1/20 = 7/20 sim;
r (3-4-5) = 20/7 = 2,85 Ohm.
Der Stromkreiswiderstand von r1 und r2 beträgt:
r (1-2) = r1 + r2 = 15 + 5 = 20 Ohm.
Die resultierende Leitfähigkeit und der Widerstand zwischen den Punkten A und B sind jeweils gleich: 1 / rAB = 1 / r (3-4-5) + 1 / r (1-2) = 7/20 + 1/20 = 8/20 sim ; rAB = 20/8 = 2,5 Ohm.
Der resultierende Widerstand des gesamten Stromkreises beträgt r = rAB + r6 = 2,5 + 7,5 = 10 Ohm.
Der resultierende Strom beträgt I = U / r = 24/10 = 2,4 A.
Die Spannung zwischen den Punkten A und B ist gleich der Quellenspannung U minus dem Spannungsabfall am Widerstand r6
UAB = U-I ∙ r6 = 24-(2,4 ∙ 7,5) = 6V.
Der Widerstand r4 ist an diese Spannung angeschlossen, sodass der durch ihn fließende Strom gleich ist:
I4 = UAB / r4 = 6/10 = 0,6A.
Die Widerstände r1 und r2 haben einen gemeinsamen Spannungsabfall UAB, daher beträgt der Strom durch r1:
I1 = UAB / r (1-2) = 6/20 = 0,3 A.
Spannungsabfall am Widerstand r1
Ur1 = I1 ∙ r1 = 0,3 ∙ 15 = 4,5 V.
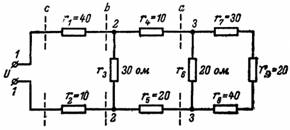
7. Wie hoch sind der resultierende Widerstand und der resultierende Strom im Stromkreis von Abb. 7 wenn die Quellenspannung U = 220 V beträgt?
Reis. 7.
Wir beginnen mit der Schaltung rechts von den Knoten 3 und 3. Die Widerstände r7, r8, r9 sind daher in Reihe geschaltet
r (7-8-9) = r7 + r8 + r9 = 30 + 40 + 20 = 90 Ohm.
Parallel zu diesem Widerstand ist ein Widerstand r6 geschaltet, so dass der resultierende Widerstand am Knoten 3 und 3 (Abschnitt a)
ra = (r6 ∙ r (7-8-9)) / (r6 + r (7-8-9)) = (20 ∙ 90) / (20 + 90) = 1800/110 = 16,36 Ohm.
Die Widerstände r4 und r5 sind mit dem Widerstand ra in Reihe geschaltet:
r (4-5-a) = 10 + 20 + 16,36 = 46,36 Ohm.
Resultierender Widerstand der Knoten 2 und 2 (Abschnitt b)
rb = (r (4-5-a) ∙ r3) / (r (4-5-a) + r3) = (46,36 ∙ 30) / (46,36 + 30) = 1390,8 / 76, 36 = 18,28 Ohm.
Der resultierende Widerstand des gesamten Stromkreises beträgt r = r1 + rb + r2 = 40 + 18,28 + 10 = 68,28 Ohm.
Der resultierende Strom beträgt I = U / r = 220 / 68,28 = 3,8 A.