Möglicher Schaltplan
 Als Potentialdiagramm bezeichnet man eine grafische Darstellung der Verteilung des elektrischen Potentials entlang eines geschlossenen Kreislaufs, abhängig vom Widerstand der im ausgewählten Kreislauf enthaltenen Abschnitte.
Als Potentialdiagramm bezeichnet man eine grafische Darstellung der Verteilung des elektrischen Potentials entlang eines geschlossenen Kreislaufs, abhängig vom Widerstand der im ausgewählten Kreislauf enthaltenen Abschnitte.
Für die Erstellung eines Potentialdiagramms wird ein geschlossener Regelkreis gewählt. Dieser Stromkreis ist so in Abschnitte unterteilt, dass es pro Abschnitt einen Verbraucher bzw. eine Energiequelle gibt. Grenzpunkte zwischen Abschnitten müssen mit Buchstaben oder Zahlen gekennzeichnet sein.
Ein Punkt der Schleife ist willkürlich geerdet, sein Potential wird bedingt als Null betrachtet. Wenn man die Kontur im Uhrzeigersinn von einem Punkt mit Nullpotenzial aus umrundet, ist das Potenzial jedes nachfolgenden Grenzpunkts als die algebraische Summe des Potenzials des vorherigen Punktes und der Potenzialänderung zwischen diesen benachbarten Punkten definiert.

Befindet sich am Objekt eine EMF-Quelle, dann ist die Potentialänderung hier numerisch gleich dem EMF-Wert dieser Quelle. Wenn die Umgehungsrichtung der Schleife und die EMF-Richtung übereinstimmen, ist die Potentialänderung positiv, andernfalls negativ.
Nach der Berechnung der Potentiale aller Punkte wird ein Potentialdiagramm in einem rechtwinkligen Koordinatensystem erstellt. Auf der Abszissenachse sind maßstabsgetreu die Widerstände der Abschnitte in der Reihenfolge ihres Zusammentreffens beim Überqueren der Kontur aufgetragen, auf der Ordinate die Potentiale der entsprechenden Punkte. Das Potenzialdiagramm beginnt bei Nullpotenzial und endet nach dem Durchlaufen.
Erstellen Sie einen möglichen Schaltplan
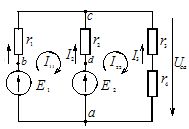
In diesem Beispiel erstellen wir ein Potentialdiagramm für die erste Schleife des Stromkreises, dessen Diagramm in Abbildung 1 dargestellt ist.
Reis. 1. Diagramm eines komplexen Stromkreises
Die betrachtete Schaltung umfasst zwei Netzteile E1 und E2, sowie zwei Stromverbraucher r1, r2.
Wir unterteilen diese Kontur in Abschnitte, deren Grenzen durch die Buchstaben a, b, c, d gekennzeichnet sind. Wir erden Punkt a, wobei wir konventionell davon ausgehen, dass sein Potenzial Null ist, und umkreisen die Kontur von diesem Punkt aus im Uhrzeigersinn. Daher ist φα = 0.
Der nächste Punkt auf dem Pfad, der die Kontur kreuzt, ist Punkt b. Die EMF-Quelle E1 befindet sich im Abschnitt ab. Wenn wir uns in diesem Abschnitt vom negativen zum positiven Pol der Quelle bewegen, erhöht sich das Potenzial um den Wert E1:
φb = φa + E1 = 0 + 24 = 24 V
Beim Übergang von Punkt b zu Punkt c verringert sich das Potential um die Größe des Spannungsabfalls am Widerstand r1 (die Bypass-Richtung der Schleife stimmt mit der Richtung des Stroms im Widerstand r1 überein):
φc = φb — Az1r1 = 24 — 3 x 4 = 12V
Wenn Sie zu Punkt d gehen, erhöht sich das Potenzial um den Betrag des Spannungsabfalls am Widerstand r2 (in diesem Abschnitt ist die Stromrichtung entgegengesetzt zur Richtung des Schleifenbypasses):
φd = φ° C + I2r2 = 12 + 0 NS 4 = 12 V
Das Potential von Punkt a ist um den Wert der EMF der Quelle E2 geringer als das Potential von Punkt d (die Richtung der EMF ist entgegengesetzt zur Richtung der Umgehung des Stromkreises):
φa = φd — E2 = 12 — 12 = 0
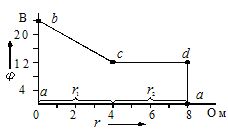
Aus den Ergebnissen der Berechnungen wird ein Potenzialdiagramm erstellt. Auf der Abszissenachse ist der Widerstand der Abschnitte in Reihe aufgetragen, wie er wäre, wenn der Stromkreis von einem Punkt mit Nullpotential umgeben wäre. Auf der Ordinate sind die zuvor berechneten Potentiale der entsprechenden Punkte aufgetragen (Abb. 2).
Zeichnung 2… Potenzialkonturdiagramm
Patskevich V.A.