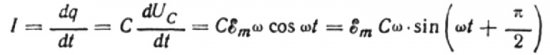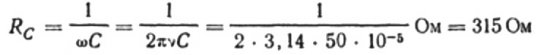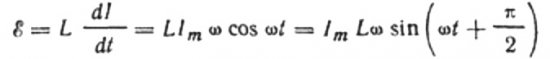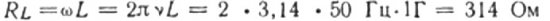Kapazitiver und induktiver Widerstand in einem Wechselstromkreis

Wenn wir einen Kondensator in einen Gleichstromkreis einbinden, stellen wir fest, dass er einen unendlichen Widerstand hat, weil ein Gleichstrom einfach nicht durch das Dielektrikum zwischen den Platten fließen kann, da ein Dielektrikum per Definition keinen direkten elektrischen Strom leitet.

Ein Kondensator unterbricht den Gleichstromkreis. Wenn aber nun derselbe Kondensator in den Wechselstromkreis geschaltet wird, dann stellt sich heraus, dass sein Kondensator nicht vollständig kaputt zu sein scheint, er wechselt einfach und lädt sich auf, das heißt, die elektrische Ladung bewegt sich und der Strom im externen Stromkreis ist gepflegt.

Basierend auf Maxwells Theorie können wir in diesem Fall sagen, dass der Wechselleitungsstrom im Inneren des Kondensators immer noch geschlossen ist, nur in diesem Fall – durch den Vorstrom. Dies bedeutet, dass der Kondensator im Wechselstromkreis als eine Art Widerstand mit endlichem Wert fungiert. Dieser Widerstand wird aufgerufen kapazitiv.

Die Praxis zeigt seit langem, dass die Menge des durch einen Leiter fließenden Wechselstroms von der Form dieses Leiters und von den magnetischen Eigenschaften des ihn umgebenden Mediums abhängt.Bei einem geraden Draht ist der Strom am größten, und wenn derselbe Draht zu einer Spule mit vielen Windungen gewickelt wird, ist der Strom geringer.

Und wenn ein ferromagnetischer Kern in dieselbe Spule eingeführt wird, sinkt der Strom noch weiter. Deshalb stellt der Draht Wechselstrom nicht nur mit einem ohmschen (aktiven) Widerstand zur Verfügung, sondern abhängig von der Induktivität des Drahtes auch mit einem zusätzlichen Widerstand. Dieser Widerstand wird als Widerstand bezeichnet induktiv.

Seine physikalische Bedeutung besteht darin, dass ein sich ändernder Strom in einem Leiter mit einer bestimmten Induktivität eine EMK der Selbstinduktion in diesem Leiter auslöst, die dazu neigt, Änderungen im Strom zu verhindern, d. h. den Strom zu reduzieren. Dies entspricht einer Erhöhung des Widerstands des Drahtes.

Kapazität im Wechselstromkreis

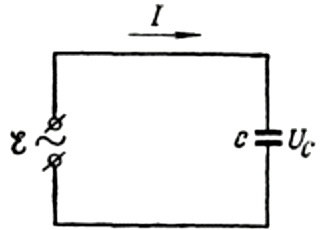
Lassen Sie uns zunächst ausführlicher über den kapazitiven Widerstand sprechen. Angenommen, ein Kondensator mit der Kapazität C ist an eine sinusförmige Wechselstromquelle angeschlossen, dann wird die EMF dieser Quelle durch die folgende Formel beschrieben:

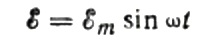
Den Spannungsabfall über den Anschlussdrähten vernachlässigen wir, da dieser meist sehr gering ist und bei Bedarf separat berücksichtigt werden kann. Nehmen wir nun an, dass die Spannung an den Kondensatorplatten gleich der Wechselstromquellenspannung ist. Dann:

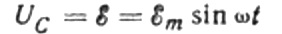
Die Ladung eines Kondensators hängt zu jedem Zeitpunkt von seiner Kapazität und der Spannung zwischen seinen Platten ab. Unter Berücksichtigung der oben erwähnten bekannten Quelle erhalten wir dann einen Ausdruck zum Ermitteln der Ladung auf den Kondensatorplatten anhand der Quellenspannung:

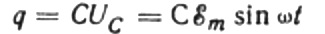
Wenn sich die Ladung des Kondensators für eine verschwindend kleine Zeitspanne dt um dq ändert, fließt ein Strom I durch die Drähte von der Quelle zum Kondensator, der gleich ist:

Der Wert der aktuellen Amplitude ist gleich:

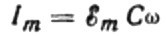
Dann lautet der endgültige Ausdruck für den Strom:

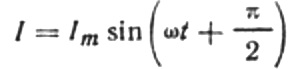
Schreiben wir die aktuelle Amplitudenformel wie folgt um:

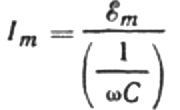
Dieses Verhältnis ist das Ohmsche Gesetz, bei dem der Kehrwert des Produkts aus Kreisfrequenz und Kapazität die Rolle des Widerstands spielt, und ist eigentlich ein Ausdruck für die Ermittlung der Kapazität eines Kondensators in einem sinusförmigen Wechselstromkreis:

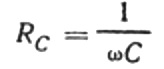
Das bedeutet, dass der kapazitive Widerstand umgekehrt proportional zur Kreisfrequenz des Stroms und der Kapazität des Kondensators ist. Die physikalische Bedeutung dieser Abhängigkeit ist leicht zu verstehen.

Je größer die Kapazität des Kondensators im Wechselstromkreis und je häufiger sich die Richtung des Stroms in diesem Stromkreis ändert, desto mehr Gesamtladung fließt pro Zeiteinheit durch den Querschnitt der Drähte, die den Kondensator mit der Wechselstromquelle verbinden. Das bedeutet, dass der Strom proportional zum Produkt aus Kapazität und Kreisfrequenz ist.

Berechnen wir zum Beispiel die Kapazität eines Kondensators mit einer elektrischen Kapazität von 10 Mikrofarad für einen sinusförmigen Wechselstromkreis mit einer Frequenz von 50 Hz:

Bei einer Frequenz von 5000 Hz hätte derselbe Kondensator einen Widerstand von etwa 3 Ohm.

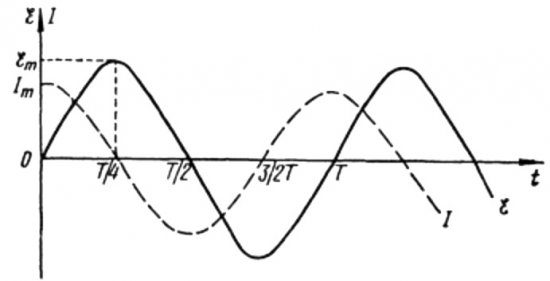
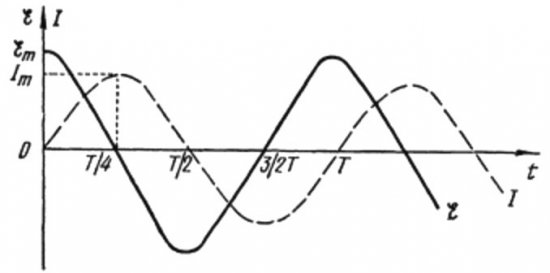
Aus den obigen Formeln wird deutlich, dass sich Strom und Spannung in einem Wechselstromkreis mit einem Kondensator immer in verschiedenen Phasen ändern. Die Stromphase eilt der Spannungsphase um pi/2 (90 Grad) voraus. Das bedeutet, dass der zeitliche Maximalstrom immer eine Viertelperiode früher liegt als die Maximalspannung. Somit eilt der Strom am kapazitiven Widerstand der Spannung um ein Viertel der Zeitperiode oder um 90 Grad in der Phase voraus.

Lassen Sie uns die physikalische Bedeutung dieses Phänomens erklären.Im ersten Moment ist der Kondensator vollständig entladen, sodass bereits die geringste an ihn angelegte Spannung die Ladungen auf den Platten des Kondensators verschiebt und einen Strom erzeugt.

Wenn sich der Kondensator auflädt, steigt die Spannung an seinen Platten, was einen weiteren Ladungsfluss verhindert, sodass der Strom im Stromkreis trotz weiterer Erhöhungen der an den Platten angelegten Spannung abnimmt.

Das heißt, wenn der Strom zu Beginn maximal war, stoppt der Strom vollständig, wenn die Spannung nach einer Viertelperiode ihr Maximum erreicht.

Zu Beginn der Periode ist der Strom maximal und die Spannung minimal und beginnt anzusteigen. Nach einem Viertel der Periode erreicht die Spannung jedoch ein Maximum, der Strom ist zu diesem Zeitpunkt jedoch bereits auf Null gesunken. Es stellt sich also heraus, dass die Spannung der Spannung um ein Viertel der Periode vorauseilt.

Induktiver Wechselstromwiderstand

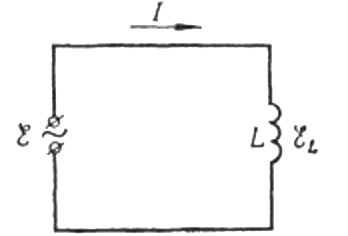
Nun zurück zum induktiven Widerstand. Nehmen Sie an, dass ein sinusförmiger Wechselstrom durch eine Induktivitätsspule fließt. Es kann ausgedrückt werden als:

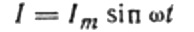
Der Strom entsteht durch die an der Spule anliegende Wechselspannung. Dies bedeutet, dass an der Spule eine EMF der Selbstinduktion auftritt, die wie folgt ausgedrückt wird:

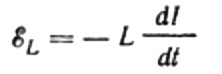
Auch hier vernachlässigen wir den Spannungsabfall an den Drähten, die die EMF-Quelle mit der Spule verbinden. Ihr ohmscher Widerstand ist sehr gering.

Die an die Spule angelegte Wechselspannung soll zu jedem Zeitpunkt vollständig durch die entstehende EMK der Selbstinduktion ausgeglichen werden, die ihr in der Größe, aber in der entgegengesetzten Richtung entspricht:

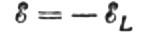
Dann haben wir das Recht zu schreiben:

Da die Amplitude der an die Spule angelegten Spannung beträgt:

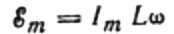
wir bekommen:

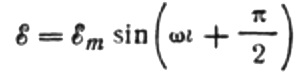
Lassen Sie uns den maximalen Strom wie folgt ausdrücken:

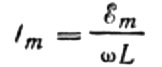
Dieser Ausdruck ist im Wesentlichen das Ohmsche Gesetz. Die Rolle des Widerstands spielt hier eine Größe gleich dem Produkt aus Induktivität und Kreisfrequenz und ist nichts anderes als der induktive Widerstand der Induktivität:

Der induktive Widerstand ist also proportional zur Induktivität der Spule und der Kreisfrequenz des Wechselstroms durch diese Spule.

Dies ist auf die Tatsache zurückzuführen, dass der induktive Widerstand auf den Einfluss der Selbstinduktions-EMF auf die Quellenspannung zurückzuführen ist. Selbstinduktions-EMF neigt dazu, den Strom zu reduzieren und erzeugt daher Widerstand im Stromkreis. Die Größe der EMK der Selbstinduktion ist bekanntlich proportional zur Induktivität der Spule und der Änderungsrate des durch sie fließenden Stroms.

Berechnen wir zum Beispiel den induktiven Widerstand einer Spule mit einer Induktivität von 1 H, die in einen Stromkreis mit einer Stromfrequenz von 50 Hz eingebunden ist:

Wenn die Frequenz des Balls 5000 Hz betragen würde, würde der Widerstand derselben Spule etwa 31.400 Ohm betragen. Denken Sie daran, dass der ohmsche Widerstand des Spulendrahts normalerweise einige Ohm beträgt.

Aus den obigen Formeln ist ersichtlich, dass die Änderungen des Stroms durch die Spule und der Spannung darin in verschiedenen Phasen auftreten und die Phase des Stroms immer kleiner als die Phase der Spannung bei pi / 2 ist. Daher ist die Der maximale Strom tritt eine Viertelperiode später auf als die maximale Belastung einsetzt.

Beim induktiven Widerstand eilt der Strom aufgrund der Bremswirkung der selbstinduzierten EMK der Spannung um 90 Grad nach, wodurch verhindert wird, dass sich der Strom ändert (sowohl zunimmt als auch abnimmt), sodass später im Stromkreis mit der Spule der maximale Strom beobachtet wird als die maximale Spannung.

Kombinierte Wirkung von Spule und Kondensator

Wenn Sie eine Spule mit einem Kondensator in Reihe mit einem Wechselstromkreis schalten, verschiebt die Spulenspannung die Kondensatorspannung zeitlich um eine halbe Periode, also um 180 Grad in der Phase.

Man nennt kapazitiven und induktiven Widerstand Reaktanten… Beim reaktiven Widerstand wird keine Energie aufgewendet wie beim aktiven Widerstand. Die im Kondensator gespeicherte Energie wird regelmäßig an die Quelle zurückgegeben, wenn das elektrische Feld im Kondensator verschwindet.

Das Gleiche gilt auch für eine Spule: Da das Magnetfeld der Spule durch den Strom erzeugt wird, sammelt sich die darin enthaltene Energie während eines Viertels der Periode an und kehrt im nächsten Viertel der Periode zur Quelle zurück. In diesem Artikel haben wir über sinusförmigen Wechselstrom gesprochen, für den diese Vorschriften strikt eingehalten werden.

In Wechselstrom-Sinuskreisen spricht man von Kerninduktivitäten erstickendwerden traditionell zur Strombegrenzung eingesetzt. Ihr Vorteil gegenüber Rheostaten besteht darin, dass Energie nicht in großen Mengen als Wärme verloren geht.