Ohmsches Gesetz für einen Magnetkreis
Gäbe es keine magnetischen Flüsse, gäbe es die moderne Elektrotechnik wohl kaum. Der Betrieb von Generatoren und Elektromotoren, Elektromagneten und Transformatoren, Messgeräten und Hall-Sensoren basiert auf der Nutzung des Magnetfeldes und den Eigenschaften des magnetischen Flusses.
Um den magnetischen Fluss zu konzentrieren und zu verstärken, greifen sie auf den Einsatz ferromagnetischer Materialien zurück. Es entstehen ferromagnetische Werkstoffe Magnetkerne — Körper der erforderlichen Formen und Größen, Kerne zum Lenken von Magnetflüssen der einen oder anderen Größe in die erforderliche Richtung. Solche Körper, in denen geschlossene magnetische Induktionslinien verlaufen, werden Magnetkreise genannt.

Die bekannten Eigenschaften des Magnetfeldes ermöglichen die Berechnung der magnetischen Flüsse in verschiedenen Magnetkreisen. Für die praktische Arbeit ist es jedoch viel bequemer, auf allgemeine Konsequenzen und Gesetze magnetischer Kreise zurückzugreifen, die aus den Gesetzen des Magnetfelds abgeleitet sind, anstatt diese Gesetze jedes Mal direkt anzuwenden. Die Anwendung bestimmter Regeln auf Magnetkreise ist für die Lösung typischer praktischer Probleme bequemer.
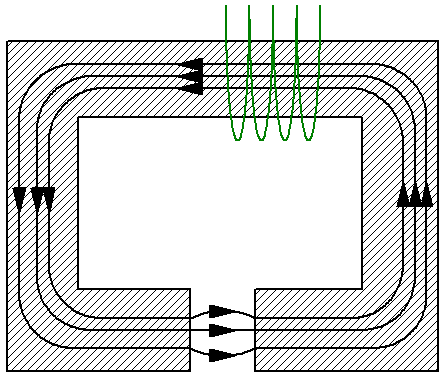
Betrachten Sie beispielsweise einen einfachen Magnetkreis, der aus einem unverzweigten Joch mit dem Querschnitt S besteht, das wiederum aus einem Material mit besteht Durchlässigkeit mu… Das Joch hat einen nichtmagnetischen Spalt mit der gleichen Fläche S, zum Beispiel Luft, und die magnetische Permeabilität im Spalt – mu1 – unterscheidet sich von der magnetischen Permeabilität des Jochs. Hier können Sie sich die mittlere Induktionslinie ansehen und den Satz der magnetischen Spannung darauf anwenden:

Da die magnetischen Induktionslinien im gesamten Stromkreis kontinuierlich sind, ist die Größe des magnetischen Flusses sowohl im Joch als auch im Spalt gleich. Jetzt verwenden wir die Formeln für magnetische Induktion B und für den magnetischen Fluss F, um die Stärke H des Magnetfelds in Form des magnetischen Flusses F auszudrücken.
Der nächste Schritt besteht darin, die resultierenden Ausdrücke in die obige Formel des Magnetflusssatzes einzusetzen:
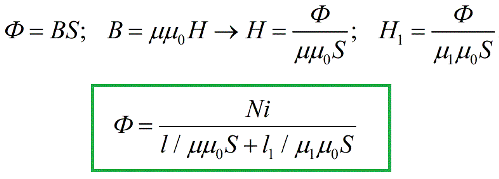
Wir haben eine Formel erhalten, die der in der Elektrotechnik bekannten sehr ähnlich ist Ohmsches Gesetz für einen Abschnitt eines geschlossenen Stromkreises, und die Rolle der EMF spielt hier die Größe iN, die in Analogie zur elektromotorischen Kraft magnetomotorische Kraft (oder MDF) genannt wird. Im SI-System wird die magnetomotorische Kraft in Ampere gemessen.
Die Summe im Nenner ist nichts anderes als eine Analogie zum gesamten elektrischen Widerstand eines Stromkreises und wird für einen magnetischen Kreis entsprechend als magnetischer Gesamtwiderstand bezeichnet. Die Terme im Nenner sind die magnetischen Widerstände einzelner Abschnitte des Magnetkreises.
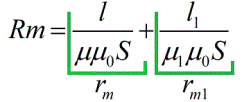
Magnetische Widerstände hängen von der Länge des Magnetkreises, seiner Querschnittsfläche und der magnetischen Permeabilität ab (ähnlich der elektrischen Leitfähigkeit für das übliche Ohmsche Gesetz).Als Ergebnis können Sie die Formel des Ohmschen Gesetzes nur für einen Magnetkreis schreiben:

Das heißt, die Formulierung des Ohmschen Gesetzes in Bezug auf einen magnetischen Kreis klingt wie folgt: „In einem magnetischen Kreis ohne Verzweigung ist der magnetische Fluss gleich dem Quotienten der Division von MDS durch den gesamten magnetischen Widerstand des Kreises.“
Aus den Formeln geht hervor, dass der magnetische Widerstand im Nordosten wird in Weber-Ampere gemessen und der gesamte magnetische Widerstand eines Magnetkreises ist numerisch gleich der Summe der magnetischen Widerstände der Teile dieses Magnetkreises.
Die beschriebene Situation gilt für einen unverzweigten Magnetkreis, der aus beliebig vielen Teilen besteht, vorausgesetzt, dass der magnetische Fluss nacheinander alle diese Teile durchdringt. Wenn die Magnetkerne in Reihe geschaltet sind, ergibt sich der gesamte magnetische Widerstand durch Addition der magnetischen Widerstände der Teile.
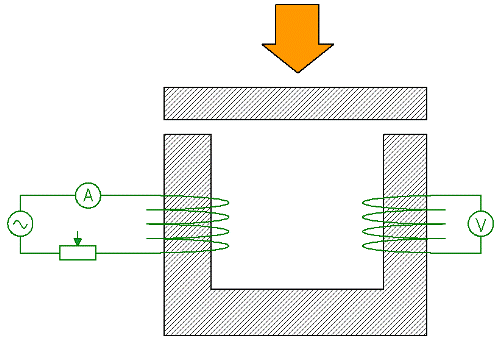
Betrachten Sie nun ein Experiment, das die Auswirkung der Reluktanz von Teilen eines Stromkreises auf die Gesamtreluktanz eines Stromkreises demonstriert. Ein U-förmiger Magnetkreis wird durch Spule 1 magnetisiert, die durch ein Amperemeter und einen Rheostat mit Wechselstrom gespeist wird. In der Sekundärwicklung 2 wird eine EMF induziert, und die Messwerte des an die Wicklung angeschlossenen Voltmeters sind, wie Sie wissen, proportional zum Magnetfluss im Magnetkreis.
Wenn Sie nun den Strom in der Primärwicklung durch Regulierung mit einem Rheostat unverändert lassen und gleichzeitig die Eisenplatte gegen den darüber liegenden Magnetkreis drücken, wird der Gesamtmagnetwiderstand des Kreises stark reduziert, der Messwert des Voltmeter erhöht sich entsprechend.
Natürlich sind die oben genannten Begriffe wie „Magnetowiderstand“ und „magnetomotorische Kraft“ formale Konzepte, da sich im magnetischen Fluss nichts bewegt, es keine sich bewegenden Teilchen gibt, es sich lediglich um eine visuelle Darstellung (wie ein Flüssigkeitsströmungsmodell) handelt ein klareres Verständnis der Gesetze...
Die physikalische Bedeutung des obigen Experiments und anderer ähnlicher Experimente besteht darin, zu verstehen, wie sich die Einführung nichtmagnetischer Lücken und magnetischer Materialien in den Magnetkreis auf den Magnetfluss im Magnetkreis auswirkt.
Indem wir beispielsweise einen Magneten in einen magnetischen Kreis einbringen, fügen wir den bereits im Kreis enthaltenen Körpern zusätzliche molekulare Ströme hinzu, die zusätzliche magnetische Flüsse einleiten. Formale Konzepte wie „magnetischer Widerstand“ und „magnetomotorische Kraft“ erweisen sich bei der Lösung eines praktischen Problems als sehr praktisch, weshalb sie in der Elektrotechnik erfolgreich eingesetzt werden.
