Gesetz der Energieerhaltung

Die moderne Physik kennt viele Arten von Energie, die mit der Bewegung oder unterschiedlichen gegenseitigen Anordnung einer Vielzahl materieller Körper oder Teilchen verbunden sind. Beispielsweise hat jeder sich bewegende Körper eine kinetische Energie, die proportional zum Quadrat seiner Geschwindigkeit ist. Diese Energie kann sich ändern, wenn die Geschwindigkeit des Körpers zunimmt oder abnimmt. Ein über dem Boden angehobener Körper weist eine potentielle Gravitationsenergie auf, die sich in der Höhe des Körpers durch drei Änderungen verändert.

Stationäre elektrische Ladungen, die in einiger Entfernung voneinander sind, haben eine elektrostatische potentielle Energie, entsprechend der Tatsache, dass sich die Ladungen nach dem Coulombschen Gesetz entweder anziehen (wenn sie unterschiedliche Vorzeichen haben) oder sich mit einer Kraft abstoßen, die umgekehrt proportional zum Quadrat ist der Abstand zwischen ihnen.

Kinetische und potentielle Energie besitzen Moleküle, Atome und Teilchen sowie ihre Bestandteile – Elektronen, Protonen, Neutronen usw. in Form mechanischer Arbeit, im Fluss von elektrischem Strom, in der Wärmeübertragung, in der Änderung des inneren Zustands von Körpern, in der Ausbreitung elektromagnetischer Wellen usw.

Vor mehr als 100 Jahren wurde ein grundlegendes physikalisches Gesetz aufgestellt, nach dem Energie nicht verschwinden oder aus dem Nichts entstehen kann. Sie kann nur von einem Typ zum anderen wechseln…. Dieses Gesetz wird Energieerhaltungssatz genannt.

In den Werken von A. Einstein wird dieses Gesetz wesentlich weiterentwickelt. Einstein begründete die Austauschbarkeit von Energie und Masse und erweiterte dadurch die Interpretation des Energieerhaltungssatzes, der heute allgemein als Energie- und Massenerhaltungssatz bezeichnet wird.

Gemäß Einsteins Theorie hängt jede Änderung der Energie dE des Körpers mit einer Änderung seiner Masse dm über die Formel dE = dmc2 zusammen, wobei c die Lichtgeschwindigkeit im Vakuum von 3 x 108 Miss ist.

Insbesondere aus dieser Formel folgt, dass, wenn infolge eines Prozesses die Masse aller am Prozess beteiligten Körper um 1 g abnimmt, die Energie 9×1013 J beträgt, was 3000 Tonnen entspricht Standardkraftstoff.

Diese Verhältnisse sind für die Analyse nuklearer Transformationen von größter Bedeutung. Bei den meisten makroskopischen Prozessen kann die Massenänderung vernachlässigt werden und nur vom Energieerhaltungssatz gesprochen werden.

Lassen Sie uns die Energieumwandlungen an einem konkreten Beispiel verfolgen. Betrachten Sie die gesamte Kette der Energieumwandlungen, die zur Herstellung eines beliebigen Teils auf einer Drehmaschine erforderlich sind (Abb. 1). Die Anfangsenergie 1, deren Menge wir als 100 % annehmen, entsteht durch die vollständige Verbrennung einer bestimmten Menge fossilen Brennstoffs. Daher sind in unserem Beispiel 100 % der Anfangsenergie in den Produkten der Kraftstoffverbrennung enthalten, die eine hohe Temperatur (ca. 2000 K) haben.

Die Verbrennungsprodukte im Kessel des Kraftwerks geben beim Abkühlen ihre innere Energie in Form von Wärme an Wasser und Wasserdampf ab. Aus technischen und wirtschaftlichen Gründen können die Verbrennungsprodukte jedoch nicht auf Umgebungstemperatur abgekühlt werden. Sie werden bei einer Temperatur von etwa 400 K durch das Rohr in die Atmosphäre geschleudert und nehmen dabei einen Teil der ursprünglichen Energie mit. Daher werden nur 95 % der ursprünglichen Energie in die innere Energie des Wasserdampfs umgewandelt.

Der entstehende Wasserdampf gelangt in die Dampfturbine, wo seine innere Energie zunächst teilweise in kinetische Energie der Dampfstränge umgewandelt wird, die dann als mechanische Energie an den Turbinenrotor übertragen wird.

Nur ein Teil der Dampfenergie kann in mechanische Energie umgewandelt werden. Der Rest wird an das Kühlwasser abgegeben, wenn der Dampf im Kondensator kondensiert. In unserem Beispiel gingen wir davon aus, dass die auf den Turbinenrotor übertragene Energie etwa 38 % beträgt, was in etwa dem Stand der Dinge in modernen Kraftwerken entspricht.

Bei der Umwandlung mechanischer Energie in elektrische Energie aufgrund der sogenannten Durch Joule-Verluste in den Rotor- und Statorwicklungen des Generators gehen etwa 2 % der Energie verloren. Dadurch werden etwa 36 % der ursprünglichen Energie ins Netz eingespeist.

Ein Elektromotor wandelt nur einen Teil der ihm zugeführten elektrischen Energie in mechanische Energie um, um die Drehmaschine zu drehen. In unserem Beispiel werden etwa 9 % der Energie in Form von Joule-Wärme in den Motorwicklungen und Reibungswärme in seinen Lagern an die umgebende Atmosphäre abgegeben.

Somit werden nur 27 % der ursprünglichen Energie an die Arbeitsorgane der Maschine abgegeben. Aber damit sind die Energiepanne noch nicht beendet. Es stellt sich heraus, dass der größte Teil der Energie bei der Bearbeitung eines Teils für Reibung aufgewendet wird und in Form von Wärme mit der Flüssigkeit abgeführt wird, die das Teil kühlt. Theoretisch würde nur ein sehr kleiner Bruchteil (in unserem Beispiel werden 2 % angenommen) der Anfangsenergie ausreichen, um den gewünschten Teil des Originalteils zu erhalten.

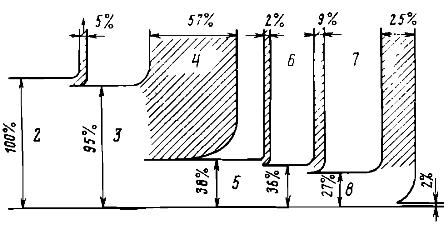
Reis. 1. Diagramm der Energieumwandlungen bei der Bearbeitung eines Werkstücks auf einer Drehmaschine: 1 – Energieverlust mit Abgasen, 2 – innere Energie der Verbrennungsprodukte, 3 – innere Energie des Arbeitsmediums – Wasserdampf, 4 – bei der Kühlung freigesetzte Wärme Wasser in einem Turbinenkondensator, 5 – mechanische Energie des Rotors eines Turbinengenerators, 6 – Verluste im elektrischen Generator, 7 – Verschwendung im elektrischen Antrieb der Maschine, 8 – mechanische Rotationsenergie der Maschine, 9 – Reibung Arbeit, die in Wärme umgewandelt wird, getrennt von der Flüssigkeit, dem Kühlteil, 10 – Erhöhung der inneren Energie des Teils und der Späne nach der Bearbeitung ...

Aus dem betrachteten Beispiel lassen sich mindestens drei sehr nützliche Schlussfolgerungen ziehen, wenn man es als einigermaßen typisch betrachtet.

Erstens geht bei jedem Schritt der Energieumwandlung ein Teil davon verloren... Diese Aussage sollte nicht als Verstoß gegen den Energieerhaltungssatz verstanden werden. Es geht aufgrund des nützlichen Effekts verloren, für den die entsprechende Transformation durchgeführt wird. Die Gesamtenergiemenge bleibt nach der Umwandlung unverändert.

Wenn der Prozess der Energieumwandlung und -übertragung in einer bestimmten Maschine oder einem bestimmten Gerät stattfindet, wird die Effizienz dieses Geräts normalerweise durch Effizienz (Effizienz)... Ein Diagramm eines solchen Geräts ist in Abb. 1 dargestellt. 2.

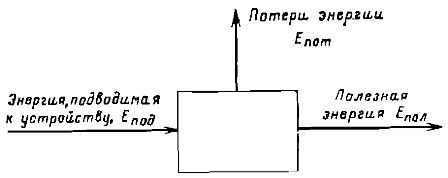
Reis. 2. Schema zur Bestimmung der Effizienz eines Geräts, das Energie umwandelt.

Unter Verwendung der in der Abbildung gezeigten Notation kann die Effizienz als Effizienz = Epol/Epod definiert werden

Es ist klar, dass in diesem Fall aufgrund des Energieerhaltungssatzes Epod = Epol + Epot gelten muss

Daher kann der Wirkungsgrad auch wie folgt geschrieben werden: Wirkungsgrad = 1 – (Epot / Epol)

Zurück zum Beispiel in FIG. 1 kann man sagen, dass der Wirkungsgrad des Kessels 95 % beträgt, der Wirkungsgrad der Umwandlung der inneren Energie des Dampfes in mechanische Arbeit 40 %, der Wirkungsgrad des elektrischen Generators 95 %, der Wirkungsgrad beträgt – der elektrische Antrieb eines Maschine — 75 %, und die Effizienz der eigentlichen Bearbeitung des Werkstücks beträgt etwa 7 %.

In der Vergangenheit, als die Gesetze der Energieumwandlung noch nicht bekannt waren, träumten die Menschen davon, ein sogenanntes Perpetuum mobile zu schaffen – ein Gerät, das nützliche Arbeit leisten würde, ohne Energie zu verbrauchen. Ein solcher hypothetischer Motor, dessen Existenz gegen den Energieerhaltungssatz verstoßen würde, wird heute als Perpetuum Mobile erster Art bezeichnet, im Gegensatz zu Perpetuum Mobile zweiter Art. Heutzutage nimmt das natürlich niemand mehr ernsthaft die Möglichkeit, ein Perpetuum mobile der ersten Art zu schaffen.

Zweitens werden alle Energieverluste letztendlich in Wärme umgewandelt, die entweder an die atmosphärische Luft oder an Wasser aus natürlichen Reservoirs abgegeben wird.

Drittens verbrauchen die Menschen am Ende nur einen kleinen Bruchteil der Primärenergie, die aufgewendet wird, um die entsprechende positive Wirkung zu erzielen.

Dies wird insbesondere bei der Betrachtung der Energietransportkosten deutlich. In der idealisierten Mechanik, die Reibungskräfte nicht berücksichtigt, benötigen bewegte Lasten in der horizontalen Ebene keine Energie.

Unter realen Bedingungen wird die gesamte von einem Fahrzeug verbrauchte Energie zur Überwindung von Reibungskräften und Luftwiderstandskräften verwendet, d. h. letztendlich wird die gesamte beim Transport verbrauchte Energie in Wärme umgewandelt. In diesem Zusammenhang sind die folgenden Zahlen interessant, die die Arbeit charakterisieren, 1 Tonne Fracht über eine Entfernung von 1 km mit verschiedenen Transportarten zu bewegen: Flugzeug – 7,6 kWh / (t-km), Auto – 0,51 kWh / (t-km) km), Zug-0,12 kWh / (t-km).

So lässt sich mit dem Luftverkehr der gleiche positive Effekt erzielen, jedoch mit einem 60-mal höheren Energieverbrauch als mit der Schiene. Natürlich führt ein hoher Energieverbrauch zu einer erheblichen Zeitersparnis, aber selbst bei gleicher Geschwindigkeit (Auto und Zug) unterscheiden sich die Energiekosten um das Vierfache.

Dieses Beispiel legt nahe, dass Menschen häufig Kompromisse bei der Energieeffizienz eingehen, um andere Ziele zu erreichen, beispielsweise Komfort, Geschwindigkeit usw. Die Energieeffizienz des Prozesses selbst interessiert uns in der Regel wenig – die allgemeine technische und Wirtschaftliche Bewertungen der Effizienz von Prozessen sind wichtig... Da jedoch die Preise für Primärenergiekomponenten steigen, wird die Energiekomponente in technischen und wirtschaftlichen Bewertungen immer wichtiger.