Spannungsfestigkeit der Isolierung. Berechnungsbeispiele

Mit einem allmählichen Anstieg der Spannung U zwischen durch ein Dielektrikum (Isolierung) getrennten Leitern, beispielsweise Kondensatorplatten oder leitenden Kabeldrähten, nimmt die Intensität (Stärke) des elektrischen Feldes im Dielektrikum zu. Auch die Stärke des elektrischen Feldes im Dielektrikum nimmt mit abnehmendem Abstand zwischen den Drähten zu.

Bei einer bestimmten Feldstärke kommt es zu einem Durchschlag im Dielektrikum, es entsteht ein Funke oder Lichtbogen und im Stromkreis entsteht ein elektrischer Strom. Die Stärke des elektrischen Feldes, bei der der Durchschlag der Isolierung auftritt, wird als elektrische Festigkeit Epr der Isolierung bezeichnet.

Die Spannungsfestigkeit ist definiert als Spannung pro mm Isolationsdicke und wird in V/mm (kV/mm) oder kV/cm gemessen. Beispielsweise beträgt die Spannungsfestigkeit von Luft zwischen glatten Platten 32 kV/cm.

Die Stärke des elektrischen Feldes in einem Dielektrikum für den Fall, dass die Leiter die Form von Platten oder Streifen haben, die durch einen gleichen Spalt getrennt sind (z. B. in einem Papierkondensator), wird nach der Formel berechnet

E = U / d,

wobei U die Spannung zwischen den Drähten V (kV) ist; d — Dicke der dielektrischen Schicht, mm (cm).

Beispiele von

1. Wie groß ist die elektrische Feldstärke im 3 cm dicken Luftspalt zwischen den Platten, wenn die Spannung zwischen ihnen U = 100 kV beträgt (Abb. 1)?

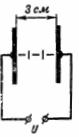
Reis. 1.

Die elektrische Feldstärke beträgt: E = U / d = 100000/3 = 33333 V/cm.

Eine solche Spannung übersteigt die Spannungsfestigkeit von Luft (32 kV/cm) und es besteht die Gefahr der Zerstörung.

Das Risiko von DC-Schäden kann verhindert werden, indem der Abstand auf beispielsweise 5 cm vergrößert wird oder eine andere, stärkere Isolierung anstelle von Luft verwendet wird, beispielsweise Elektrokarton (Abb. 2).

Reis. 2.

Elektrokarton hat eine Dielektrizitätskonstante von ε = 2 und eine Spannungsfestigkeit von 80.000 V/cm. In unserem Fall beträgt die elektrische Feldstärke in der Isolierung 33333 V. Luft kann dieser Kraft nicht standhalten, während der Elektrokarton in diesem Fall eine Durchschlagsfestigkeitsreserve von 80.000/33333 = 2,4 aufweist, da die Durchschlagsfestigkeit des Elektrokastens beträgt 80.000/32.000 = 2,5-mal so viel wie Luft.

2. Wie groß ist die elektrische Feldstärke im Dielektrikum eines 3 mm dicken Kondensators, wenn an den Kondensator eine Spannung U = 6 kV angelegt wird?

E = U / d = 6000 / 0,3 = 20000 V / cm.

3. Ein Dielektrikum mit einer Dicke von 2 mm zerfällt bei einer Spannung von 30 kV. Wie hoch war seine elektrische Stärke?

E = U / d = 30.000 / 0,2 = 150.000 V / cm = 150 kV / cm. Glas hat eine solche elektrische Festigkeit.

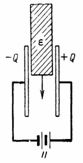
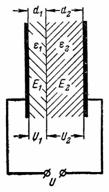
4. Der Raum zwischen den Platten des Kondensators wird mit Lagen Elektrokarton und einer Glimmerschicht gleicher Dicke gefüllt (Abb. 3). Die Spannung zwischen den Platten des Kondensators beträgt U = 10000 V. Der Elektrokarton hat eine Dielektrizitätskonstante ε1 = 2 und Glimmer ε2 = 8.Wie verteilt sich die Spannung U zwischen den Isolationsschichten und welche Stärke hat das elektrische Feld in den einzelnen Schichten?

Reis. 3.

Die Spannungen U1 und U2 an dielektrischen Schichten gleicher Dicke sind nicht gleich. Die Kondensatorspannung wird in die Spannungen U1 und U2 aufgeteilt, die umgekehrt proportional zu den Dielektrizitätskonstanten sind:

U1 / U2 = ε2 / ε1 = 8/2 = 4/1 = 4;

U1 = 4 ∙ U2.

Da U = U1 + U2, haben wir zwei Gleichungen mit zwei Unbekannten.

Setze die erste Gleichung in die zweite ein: U = 4 ∙ U2 + U2 = 5 ∙ U2.

Daher ist 10000 V = 5 ∙ U2; U2 = 2000 V; U1 = 4, U2 = 8000 V.

Obwohl die dielektrischen Schichten gleich dick sind, sind sie nicht gleich geladen. Ein Dielektrikum mit einer höheren Dielektrizitätskonstante wird weniger belastet (U2 = 2000 V) und umgekehrt (U1 = 8000 V).

Die elektrische Feldstärke E in den dielektrischen Schichten ist gleich:

E1 = U1 / d1 = 8000 / 0,2 = 40.000 V/cm;

E2 = U2 / d2 = 2000 / 0,2 = 10000 V / cm.

Der Unterschied in der Dielektrizitätskonstante führt zu einer Erhöhung der elektrischen Feldstärke. Wenn der gesamte Spalt nur mit einem Dielektrikum, zum Beispiel Glimmer oder Elektropappe, gefüllt wäre, wäre die elektrische Feldstärke geringer, da sie sich ziemlich gleichmäßig im Spalt verteilen würde:

E = U / d = (U1 + U2) / (d1 + d2) = 10000 / 0,4 = 25000 V / cm.

Daher muss auf den Einsatz aufwändiger Isolierungen mit stark unterschiedlichen Dielektrizitätskonstanten verzichtet werden. Aus dem gleichen Grund erhöht sich das Ausfallrisiko, wenn sich Luftblasen in der Isolierung bilden.

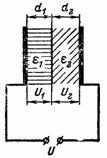
5. Bestimmen Sie die Stärke des elektrischen Feldes im Kondensatordielektrikum aus dem vorherigen Beispiel, wenn die Dicke der dielektrischen Schichten nicht gleich ist.Die Elektroplatine hat eine Dicke d1 = 0,2 mm und Glimmer d2 = 3,8 mm (Abb. 4).

Reis. 4.

Die elektrische Feldstärke verteilt sich umgekehrt proportional zu den Dielektrizitätskonstanten:

E1 / E2 = ε2 / ε1 = 8/2 = 4.

Da E1 = U1 / d1 = U1 / 0,2 und E2 = U2 / d2 = U2 / 3,8, dann ist E1 / E2 = (U1 / 0,2) / (U2 / 3,8) = (U1 ∙ 3,8) / (0,2 ∙ U2) = 19 ∙ U1 / U2.

Daher ist E1 / E2 = 4 = 19 ∙ U1 / U2, oder U1 / U2 = 4/19.

Die Summe der Spannungen U1 und U2 an den dielektrischen Schichten ist gleich der Quellenspannung U: U = U1 + U2; 10000 = U1 + U2.

Da U1 = 4/19 ∙ U2, dann 10000 = 4/10 ∙ U2 + U2 = 23/19 ∙ U2; U2 = 190.000 /23 = 8260 V; U1 = U-U2 = 1740 V.

Die Stärke des elektrischen Feldes in Glimmer beträgt E2 ∙ 8260 / 3,8≈2174 V/cm.

Glimmer hat eine elektrische Festigkeit von 80.000 V/mm und kann einer solchen Spannung standhalten.

Die elektrische Feldstärke im Elektrokarton beträgt E1 = 1740 / 0,2 = 8700 V/mm.

Elektrokarton hält einer solchen Spannung nicht stand, da seine Spannungsfestigkeit nur 8000 V/mm beträgt.

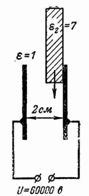
6. An zwei Metallplatten im Abstand von 2 cm wird eine Spannung von 60.000 V angelegt. Bestimmen Sie die elektrische Feldstärke im Luftspalt sowie die elektrische Feldstärke in Luft und Glas. Wenn sich Glas im Spalt befindet, fügt man eine Platte mit ein eine Dicke von 1 cm (Abb. 5).

Reis. 5.

Befindet sich zwischen den Platten nur Luft, beträgt die elektrische Feldstärke darin: E = U / d = 60.000 /2 = 30.000 V / cm.

Die Feldstärke liegt nahe an der Spannungsfestigkeit von Luft.Wird eine 1 cm dicke Glasplatte (Glasdielektrizitätskonstante ε2 = 7) in den Spalt eingebracht, so gilt E1 = U1 / d1 = U1 / 1 = U1; E2 = U2 / d2 = U2 / 1 = U2; E1 / E2 = ε2 / ε1 = 7/1 = U1 / U2;

U1 = 7 ∙ U2; U1 = 60.000-U2; 8 ∙ U2 = 60.000; U2 = 7500 V; E2 = U2 / d2 = 7500 V / cm.

Die Stärke des elektrischen Feldes im Glas beträgt E2 = 7,5 kV/cm und seine elektrische Stärke beträgt 150 kV/cm.

In diesem Fall hat das Glas einen 20-fachen Sicherheitsfaktor.

Für den Luftspalt gilt: U1 = 60.000-7500 = 52500 V; E1 = U1 / d1 = 52500 V / cm.

In diesem Fall ist die Stärke des elektrischen Feldes im Luftspalt größer als im ersten Fall ohne Glas. Nach dem Einsetzen des Glases hat die gesamte Kombination eine geringere Festigkeit als Luft allein.

Bruchgefahr besteht auch dann, wenn die Dicke der Glasplatte gleich dem Spalt zwischen den leitenden Platten ist, also 2 cm, da zwangsläufig dünne Luftspalte im Spalt entstehen, die durchstochen werden.

Die Spannungsfestigkeit des Spalts zwischen den Hochspannungsleitern muss durch Materialien mit niedriger Dielektrizitätskonstante und hoher Durchschlagsfestigkeit verstärkt werden, zum Beispiel Elektrokarton mit ε = 2. Vermeiden Sie Kombinationen von Materialien mit hoher Dielektrizitätskonstante (Glas). , Porzellan) und Luft, die durch Öl ersetzt werden müssen.