Berechnung von Potentiometer und Compound-Shunt
Konzepte und Formeln
 Ein Potentiometer ist ein variabler Widerstand mit einem Schieber, der wie in Abb. gezeigt enthalten ist.
Ein Potentiometer ist ein variabler Widerstand mit einem Schieber, der wie in Abb. gezeigt enthalten ist.
Weitere Einzelheiten finden Sie unter — Potentiometer und ihre Anwendungen
An den Punkten 1 und 2 liegt eine Spannung U an. An den Punkten 2 und 3 wird eine einstellbare Spannung abgenommen, deren Wert kleiner als U ist und von der Position des Schiebers abhängt. Spannungsteiler haben ein ähnliches Schema, sind jedoch nicht einstellbar und verfügen über keinen beweglichen Schieber.
Potentiometer, Spannungsteiler und komplexe Shunts werden mit berechnet Kirchhoffs Gesetze, wie etwa die Berechnung konventioneller Schaltungen mit Widerständen.
Beispiele von
1. Die Quellenspannung beträgt U = 24 V, der Gesamtwiderstand des Potentiometers beträgt r = 300 Ohm. Der Motor wird separat montiert, so dass r1 = 50 Ohm. Welche Spannung U1 kann an den Punkten 3 und 2 entnommen werden (Abb. 1)?
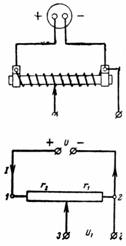
Reis. 1.
Der Strom I und die Spannung U am Widerstand r hängen durch die Formel I ∙ r = U zusammen.
Der Potentiometer-Schieber trennt einen Teil des Widerstands, d. der Widerstand r1. Der Spannungsabfall zwischen den Punkten 3 und 2 beträgt I ∙ r1 = U1.
Aus dem Verhältnis des Spannungsabfalls ergibt sich die Gleichung (I ∙ r1) / (I ∙ r) = U1 / U. Je größer der Widerstand r1, desto größer ist der Wert der Spannung U1 zwischen den Punkten 3 und 2 U1 = r1 / r ∙ U = 50/300 ∙ 24 = 4 V.
2. Das Potentiometer (Abb. 2) wird auf eine Lampe mit Widerstand r = 100 Ohm geladen. Das Potentiometer wird durch einen Schieber in zwei Teile mit r1 = 600 Ohm und r2 = 200 Ohm geteilt. Bestimmen Sie die Spannung Ul und den Lampenstrom Il.
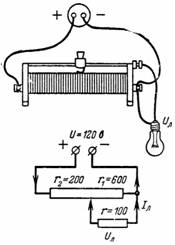
Reis. 2.
Der Strom I fließt durch den Widerstand r2 und der Strom Il fließt durch die Lampe. Durch den Widerstand r1 fließt ein Strom I-Il, der am Widerstand r1 eine Spannung erzeugt, die der Lampenspannung entspricht: (I-Il) ∙ r1 = Ul.
Andererseits ist die Lampenspannung gleich der Quellenspannung minus Spannungsabfall am Widerstand r2: U-I ∙ r2 = Ul.
Der Strom I ist gleich der Quellenspannung dividiert durch den resultierenden Widerstandswert der Reihen-Parallelschaltung der Widerstände:
I = U / (r2 + (r ∙ r1) / (r + r1)).
Wir ersetzen den Ausdruck für den Gesamtstrom der Quelle in der zweiten Gleichung:
U-U / (r2 + (r ∙ r1) / (r + r1)) ∙ r2 = Ul.
Nach der Transformation erhalten wir einen Ausdruck für die Lampenspannung:
Ul = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) ∙ r.
Wenn wir diesen Ausdruck transformieren, ausgehend von der Tatsache, dass Ul = Il ∙ r, dann erhalten wir einen Ausdruck für den Lampenstrom:
Il = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r).
Setzen Sie die Zahlenwerte in die resultierenden Gleichungen ein:
Ul = (120 ∙ 600) / (600 ∙ 200 + 600 ∙ 100 + 200 ∙ 100) ∙ 100 = 7200000/200000 = 36 V;
Il = Ul / r = 36/100 = 0,36 A.
3. Berechnen Sie die Spannung Up und den Strom Ip des Messgeräts, das an einen Teil des Potentiometers angeschlossen ist. Das Gerät hat einen Widerstand von r = 1000 Ohm. Der Verzweigungspunkt teilt den Widerstand des Teilers in r2 = 500 Ohm und r1 = 7000 Ohm (Abb. 3).Spannung an den Klemmen des Potentiometers U = 220 V.
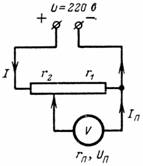
Reis. 3.
Mit den zuvor erhaltenen Formeln können wir schreiben, dass der durch das Gerät fließende Strom wie folgt ist:
In = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) = (220 ∙ 7000) / (7000 ∙ 500 + 7000 ∙ 1000 + 500 ∙ 1000)= 1540000/11000000 = 1,54 / 11 = 0,14 A.
Up = Ip ∙ r = 0,14 ∙ 1000 = 14 V.
4. Berechnen Sie die Spannung des Geräts Up, wenn es einen Strom Ip = 20 mA verbraucht und an ein Potentiometer angeschlossen ist, das in Widerstände r2 = 10 ^ 4 Ohm und r1 = 2 ∙ 10 ^ 4 Ohm aufgeteilt ist (Abb. 3).
Die Gesamtspannung im Spannungsteiler ist gleich der Summe der Spannungsabfälle in seinen Teilen (durch die Widerstände r1 und r2): U = I ∙ r2 + I1 ∙ r1; U = I ∙ r2 + Up
Der Quellstrom verzweigt sich am Motorkontaktpunkt: I = I1 + Ip; I = Upn / r1 + In.
Wir setzen den Wert des Stroms I in die Spannungsgleichung ein:
U = (Un / r1 + In) ∙ r2 + Un;
U = Uп / r1 ∙ r2 + Iп ∙ r2 + Uп;
U = Upn ∙ (r2 / r1 +1) + In ∙ r2.
Daher ist die Gerätespannung Upn = (U-In ∙ r2) / (r1 + r2) ∙ r1.
Ersetzen Sie die Zahlenwerte: Up = (220-0,02 ∙ 10000) / 30000 ∙ 20000 = 20/3 ∙ 2 = 13,3 V.
5. Eine Gleichstromquelle mit der Spannung U = 120 V versorgt die Anodenkreise des Funkempfängers über ein Potentiometer (Spannungsteiler), das zusammen mit dem Filter einen Widerstand von r = 10000 Ohm hat. Die Spannung U1 wird durch den Widerstand r2 = 8000 Ohm abgenommen. Berechnen Sie die Anodenspannung im Leerlauf und bei einem Laststrom I = 0,02 A (Abb. 4).
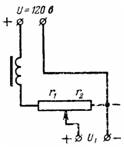
Reis. 4.
Der erste Fall ähnelt Beispiel 1:
U: U1 = r: r2;
U1 = r2 / r ∙ U = 8000/10000 ∙ 120 = 96 V.
Der zweite Fall ähnelt Beispiel 3:
U1 = (U-I ∙ r1) / r ∙ r2;
U1 = (120-0,02 ∙ 2000) / 10000 ∙ 8000 = 64 V.
Beim Laden sinkt die Spannung von 96 auf 64 V.Wird mehr Spannung benötigt, dann sollte der Schieber nach links verschoben werden, also der Widerstand r2 erhöht werden.
6. Die Spannungen Ua und Ub werden durch den Spannungsteiler entfernt. Der Gesamtwiderstand des an die Spannung U1 = 220 V angeschlossenen Spannungsteilers beträgt r = 20.000 Ohm. Wie groß ist die Spannung Ua im Widerstand r3 = 12000 Ohm bei Stromaufnahme Ia = 0,01 A und die Spannung Ub im Widerstand r2 + r3 = 18000 Ohm bei Stromaufnahme Ib = 0,02 A (Abb. 5).
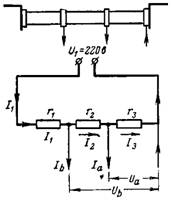
Reis. 5.
Spannungswiderstand r3
Ua = I3 ∙ r3;
Ua = (U -Ia ∙ (r1 + r2) -Ib ∙ r1) / r ∙ r3;
Ua = (220-0,01 ∙ 8000-0,02 ∙ 2000) / 20 000 ∙ 12000 = (220-80-40) / 20 ∙ 12 = 60 V.
Die Spannung Ub ist gleich der Summe aus dem Spannungsabfall Ua am Widerstand r3 und dem Spannungsabfall am Widerstand r2. Der Spannungsabfall am Widerstand r2 ist gleich I2 ∙ r2. Strom I2 = Ia + I3. Der Strom I3 kann wie in Beispiel 1 berechnet werden:
I3 = (220-80-40) / 20.000 = 0,005 A;
I2 = Ia + I3 = 0,01 + 0,005 = 0,015 A.
Spannung Ub = Ua + I2 ∙ r2 = 5 + 0,015 ∙ 6000 = 150 V.
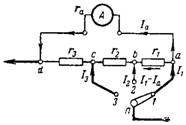
7. Berechnen Sie den kombinierten Shunt für das Milliamperemeter so, dass es bei verschiedenen Stellungen des Schalters die folgenden Messbereiche hat: I1 = 10 mA; I2 = 30mA; I3 = 100mA. Das Shunt-Verbindungsdiagramm ist in Abb. dargestellt. 6. Innenwiderstand des Gerätes ra = 40 Ohm. Eigenmessbereich des Milliamperemeters 2 mA.
Reis. 6.
Bei der Messung des Stroms I≤2mA wird der Shunt abgeschaltet.
a) Bei der Messung des Stroms I = 10 mA steht der Schalter in Stellung 1 und durch alle Shunt-Widerstände fließt ein Strom von 10-2 = 8 mA. Der Spannungsabfall am Shunt-Widerstand Ush und am Gerät Ua zwischen den Punkten d und a muss gleich sein
Ush = Ua;
(I1-Ia) ∙ (r1 + r2 + r3) = Ia ∙ ra;
0,008 ∙ (r1 + r2 + r3) = 0,002 ∙ 40.
b) Bei der Messung des Stroms I2 = 30 mA steht der Schalter in Position 2. Der gemessene Strom teilt sich am Punkt b. Bei Vollausschlag des Gerätezeigers fließt der Strom Ia = 2 mA durch den Widerstand r1 und das Gerät ra.
Der Rest des Stroms I2-Ia fließt durch die Widerstände r2 und r3. Die Ströme erzeugen in den beiden Zweigen zwischen den Punkten d und b den gleichen Spannungsabfall:
(I2-Ia) ∙ (r2 + r3) = Ia ∙ r1 + Ia ∙ ra;
(0,03-0,002) ∙ (r2 + r3) = 0,002 ∙ (r1 + 40).
c) In ähnlicher Weise führen wir die Berechnung bei der Erweiterung des Messbereichs auf I3 = 100 mA durch. Der Strom I3-Ia fließt durch den Widerstand r3 und der Strom Ia durch die Widerstände r1, r2, ra. Die Spannung in beiden Zweigen ist gleich: (I3-Ia) ∙ r3 = Ia ∙ r1 + Ia ∙ r2 + Ia ∙ ra;
0,098 ∙ r3 = 0,002 ∙ (r1 + r2 + 40).
Wir haben drei Gleichungen mit drei unbekannten Widerstandswerten r1, r2 und r3 erhalten.
Wir multiplizieren alle Gleichungen mit 1000 und wandeln sie um:
r1 + r2 + r3 = 10;
14 ∙ (r2 + r3) -r1 = 40;
49 ∙ r3-r1-r2 = 40.
Fügen wir die erste und dritte Gleichung hinzu: 50 ∙ r3 = 50;
r3 = 50/50 = 1 Ohm.
Addieren wir die erste und zweite Gleichung: 15 ∙ r2 + 15 ∙ r3 = 50;
15 ∙ r2 + 15 ∙ 1 = 50;
15 ∙ r2 = 35; r2 = 2,34 Ohm.
Setzen wir die erhaltenen Ergebnisse in die erste Gleichung ein: r1 + 35/15 + 1 = 10;
15 ∙ r1 + 35 + 15 = 150;
r1 = 100/15 = 6,66 Ohm.
Die Richtigkeit der Berechnung kann überprüft werden, indem die erhaltenen Widerstandswerte in die Gleichungen eingesetzt werden.