Berechnungen magnetischer Kreise

Bei elektrischen Maschinen und Geräten konzentriert sich der magnetische Fluss F im Magnetkreis (ferromagnetischer Kern) und den Luftspalten dieses Magnetkreises. Dieser Weg des magnetischen Flusses wird als magnetischer Kreis bezeichnet.

Ein magnetischer Kreis ist wie ein elektrischer Kreis. Der magnetische Fluss Ф ähnelt einem elektrischen Strom I, die Induktion В ähnelt einer Stromdichte, die Magnetisierungskraft (ns) Fн (H ∙ l = I ∙ ω) entspricht e. usw. mit

Im einfachsten Fall hat der Magnetkreis überall den gleichen Querschnitt und besteht aus einem homogenen magnetischen Material. Um n zu bestimmen. wobei l ∙ ω erforderlich ist, um die erforderliche Induktion B bereitzustellen, wird die entsprechende Intensität H aus der Magnetisierungskurve ermittelt und mit der mittleren Länge der magnetischen Feldlinie l multipliziert: H ∙ l = I ∙ ω = Fm.

Daraus wird der benötigte Strom I bzw. die Windungszahl ω der Spule ermittelt.

Ein komplexer Magnetkreis besteht normalerweise aus Abschnitten mit unterschiedlichen Abschnitten und magnetischen Materialien. Diese Abschnitte sind normalerweise in Reihe geschaltet, daher fließt durch jeden von ihnen der gleiche magnetische Fluss F.Die Induktion B in jedem Abschnitt hängt vom Querschnitt des Abschnitts ab und wird für jeden Abschnitt separat nach der Formel B = Φ∶S berechnet.

Für unterschiedliche Induktionswerte wird die Intensität H aus der Magnetisierungskurve ermittelt und mit der durchschnittlichen Länge der Stromleitung des entsprechenden Stromkreisabschnitts multipliziert. Summiert man die einzelnen Werke, so erhält man das Gesamtn. c. Magnetkreis:

Fm = I ∙ ω = H1 ∙ l1 + H2 ∙ l2 + H3 ∙ l3 + … was den Magnetisierungsstrom bzw. die Anzahl der Spulenwindungen bestimmt.

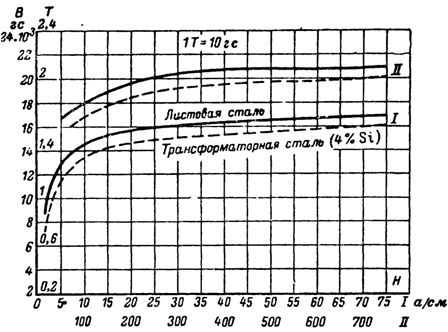
Magnetisierungskurven

Beispiele von

1. Wie groß muss der Magnetisierungsstrom I einer Spule mit 200 Windungen sein, damit n. c. erzeugt im Gusseisenring einen magnetischen Fluss Ф = 15700 Ms = 0,000157 Wb? Der durchschnittliche Radius des Gusseisenrings beträgt r = 5 cm und der Durchmesser seines Abschnitts beträgt d = 2 cm (Abb. 1).

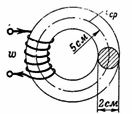
Reis. 1.

Abschnitt des Magnetkreises S = (π ∙ d ^ 2) / 4 = 3,14 cm2.

Die Induktion im Kern beträgt: B = Φ∶S = 15700∶3,14 = 5000 G.

Im MKSA-System beträgt die Induktion: B = 0,000157 Wb: 0,0000314 m2 = 0,5 T.

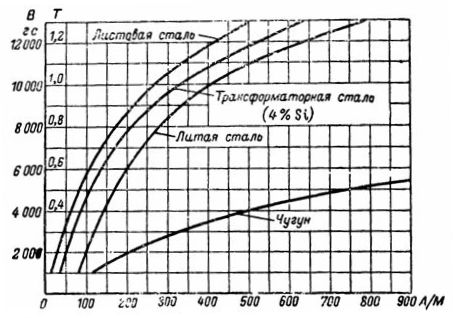
Aus der Magnetisierungskurve von Gusseisen ermitteln wir die erforderliche Stärke H von 750 A/m für B = 5000 G = 0,5 T. Die Magnetisierungsstärke ist gleich: I ∙ ω = H ∙ l = 235,5 Av.

Daher beträgt der erforderliche Strom I = (H ∙ l) / ω = 235,5 / 200 = 1,17 A.

2. Ein geschlossener Magnetkreis (Abb. 2) besteht aus Stahlplatten eines Transformators. Wie viele Windungen muss eine Spule mit einem Strom von 0,5 A haben, um im Kern einen magnetischen Fluss Ф = 160000 Ms = 0,0016 Wb zu erzeugen?

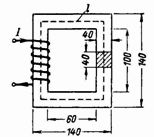
Reis. 2.

Kernabschnitt S = 4 ∙ 4 = 16 cm2 = 0,0016 m2.

Kerninduktion B = F / S = 160000/16 = 10000 Gs = 1 T.

Gemäß der Magnetisierungskurve des Transformatorstahls finden wir für B = 10.000 Gs = 1 T die Intensität H = 3,25 A/cm = 325 A/m.

Die durchschnittliche Länge der Magnetfeldlinie beträgt l = 2 ∙ (60 + 40) + 2 ∙ (100 + 40) = 480 = 0,48 m.

Magnetisierungskraft Fm = I ∙ ω = H ∙ l = 3,25 ∙ 48 = 315 ∙ 0,48 = 156 Av.

Bei einem Strom von 0,5 A beträgt die Windungszahl ω = 156 / 0,5 = 312.

3. Der in Abb. dargestellte Magnetkreis. 3 ähnelt dem Magnetkreis des vorherigen Beispiels, weist jedoch einen Luftspalt von δ = 5 mm auf. Was soll n sein. s. und den Spulenstrom so, dass der magnetische Fluss derselbe ist wie im vorherigen Beispiel, also F = 160000 Ms = 0,0016 Wb?

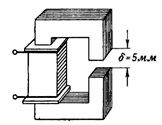
Reis. 3.

Der Magnetkreis besteht aus zwei in Reihe geschalteten Abschnitten, deren Querschnitt der gleiche ist wie im vorherigen Beispiel, also S = 16 cm2. Die Induktivität beträgt ebenfalls B = 10000 G = 1 T.

Die durchschnittliche Länge der magnetischen Stahllinie ist etwas kürzer: lс = 48-0,5 = 47,5 cm ≈0,48 m.

Die magnetische Spannung in diesem Abschnitt des Magnetkreises beträgt Hc ∙ lc = 3,25 ∙ 48≈156 Av.

Die Feldstärke im Luftspalt beträgt: Hδ = 0,8 ∙ B = 0,8 ∙ 10000 = 8000 A/cm.

Die magnetische Spannung im Querschnitt des Luftspalts Hδ ∙ δ = 8000 ∙ 0,5 = 4000 Av.

Komplette n. c. ist gleich der Summe der magnetischen Spannungen in einzelnen Abschnitten: I ∙ ω = Hс ∙ lс + Hδ ∙ δ = 156 + 4000 = 4156 Av. I = (I ∙ ω) / ω = 4156/312 = 13,3 A.

Wenn im vorherigen Beispiel der erforderliche Magnetfluss durch einen Strom von 0,5 A bereitgestellt wurde, ist für einen Magnetkreis mit einem Luftspalt von 0,5 cm ein Strom von 13 A erforderlich, um den gleichen Magnetfluss zu erhalten. Daraus ist ersichtlich, dass ein Luftspalt, selbst wenn er im Verhältnis zur Länge des Magnetkreises unbedeutend ist, das erforderliche n stark erhöht. v. und Spulenstrom.

4. Der magnetische Fluss des Transformators wird mit F = 72000 Ms berechnet. Die Berechnung von n ist erforderlich.s.und Magnetisierungsstrom der Primärwicklung mit 800 Windungen. Im Kern des Transformators befindet sich ein Spalt δ = 0,2 mm. Die Abmessungen des Transformatorkerns sind in Abb. dargestellt. 4. Querschnitt des Kerns S = 2 ∙ 3 ​​​​​​= 6 cm2 (Transformatoren mit Kernen dieser Form werden als gepanzert bezeichnet).

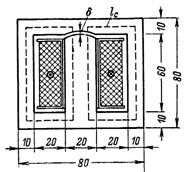
Reis. 4.

Kern- und Luftspaltinduktion B = F / S = 72000/6 = 12000 G.

Anhand der Magnetisierungskurve des Transformatorstahls für B = 12000 G ermitteln wir die Intensität: Hc = 5 A/cm.

Die durchschnittliche Länge der Magnetlinie in Stahl beträgt lс = 2 ∙ (6 + 3) = 18 cm.

Spannung im Luftspalt Hδ = 0,8 ∙ B = 9600 A/cm.

Magnetisierungskraft I ∙ ω = Hc ∙ lc + Hδ ∙ δ = 5 ∙ 18 + 9600 ∙ 0,02 = 90 + 192 = 282 Av; I = (I ∙ ω) / ω = 282/800 = 0,35 A.

Im Panzerkern teilt sich der Magnetfluss in zwei Teile auf, die entlang der Seitenstäbe geschlossen sind, deren Querschnitt S / 2 beträgt und die durchschnittliche Länge der Magnetlinie lc beträgt. Dadurch ist der Magnetkreis völlig analog zum Magnetkreis eines herkömmlichen Transformators mit einem gemeinsamen Kern S und einer Länge der Stromleitung lc.

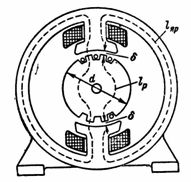
5. Der magnetische Fluss der Gleichstrommaschine F = 1280000 Mks. Der Magnetkreis enthält ein Gussstahljoch mit einer durchschnittlichen magnetischen Linienlänge là = 80 cm, einen aus Elektrostahlplatten zusammengesetzten Rotor mit einer durchschnittlichen Feldlänge là = 18 cm und zwei Luftspalte δ von jeweils 0,2 cm. = 8 ∙ 20 cm2; Rotor- und Polabschnitt Sð = 12 ∙ 20 cm2... Berechnen Sie n. p. und die Anzahl der Windungen der Polspule, wenn der maximale magnetisierende (erregende) Strom darin 1 A beträgt (Abb. 5).

Reis. 5.

Induktion im Joch und Pol Bя = Ф / Sя = 1280000/160 = 8000 G.

Die Spannung im Joch und Pol gemäß der Magnetisierungskurve von Stahlguss bei Bя = 8000 G ist gleich:

H = 2,8 A/cm.

Die Magnetisierungskraft im Abschnitt des Jochs HЯ ∙ la = 2,8 ∙ 80 = 224 Av.

Induktion im Rotor, Pol und Luftspalt Br = Ф / Ср = 1280000/240 = 5333 G.

Spannung in einem Rotor aus Stahlplatten bei Br = 5333 Gs Hrp = 0,9 A/cm,

und die magnetische Spannung des Rotorabschnitts Hð ∙ lð = 0,9 ∙ 18 = 16,2 Av.

Spannung im Luftspalt Hδ = 0,8 ∙ Bδ = 0,8 ∙ 5333 = 4266,4 A/cm.

Die magnetische Spannung im Querschnitt des Luftspalts Hδ ∙ 2 ∙ δ = 4266,4 ∙ 2 ∙ 0,2 = 1706,56 A.

Komplette n. c. gleich der Summe der magnetischen Spannungen in einzelnen Abschnitten: I ∙ ω = Hя ∙ la + Hð ∙ lð + Hδ ∙ 2 ∙ δ; I ∙ ω = 224 + 16,2 + 1706,56 = 1946,76 Av.

Die Windungszahl der beiden Polspulen beträgt ω = (I ∙ ω) / I = 1946,76 / 1≈2000.