Linearisierung der Sensoreigenschaften

Linearisierung der Sensoreigenschaften – eine nichtlineare Transformation des Sensorausgangswerts oder einer dazu proportionalen Größe (analog oder digital), die eine lineare Beziehung zwischen dem gemessenen Wert und dem ihn darstellenden Wert erreicht.

Mit Hilfe der Linearisierung ist es möglich, eine Linearität auf der Skala des sekundären Geräts zu erreichen, an das ein Sensor mit nichtlinearer Kennlinie angeschlossen ist (z. B. Thermoelement, thermischer Widerstand, Gasanalysator, Durchflussmesser usw.). Die Linearisierung der Sensoreigenschaften ermöglicht es, durch Sekundärgeräte mit digitalem Ausgang die erforderliche Messgenauigkeit zu erreichen. Dies ist in manchen Fällen beim Anschluss von Sensoren an Aufzeichnungsgeräte oder bei der Durchführung mathematischer Operationen mit dem Messwert (z. B. Integration) erforderlich.

Bezogen auf die Gebercharakteristik wirkt die Linearisierung wie eine inverse funktionale Transformation.Wenn die Kennlinie des Sensors als y = F (a + bx) dargestellt wird, wobei x der Messwert ist, a und b Konstanten sind, dann sollte die Kennlinie des in Reihe mit dem Sensor geschalteten Linearisierers aussehen (Abb. 1). wie folgt: z = kF (y), wobei F die Umkehrfunktion von F ist.

Infolgedessen ist die Ausgabe des Linearisierers z = kF(F (a + bx)) = a ' + b'x, d. h. eine lineare Funktion des Messwerts.

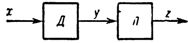
Reis. 1. Verallgemeinertes Linearisierungsblockdiagramm: D – Sensor, L – Linearisierer.

Darüber hinaus wird durch die Skalierung die Abhängigkeit z auf die Form z' = mx reduziert, wobei m der entsprechende Skalierungsfaktor ist. Erfolgt die Linearisierung kompensatorisch, also auf Basis eines Servosystems wie in Abb. 2, dann sollte die Kennlinie des linearisierenden Funktionswandlers der Kennlinie des Sensors z = cF (a + bx) ähnlich sein, da der linearisierte Wert des Messwerts vom Eingang des Wandlers des Funktionslinearisators und dessen entnommen wird Der Ausgang wird mit dem Ausgangswert des Sensors verglichen.

Ein charakteristisches Merkmal von Linearisierern als Funktionswandler ist eine relativ enge, auf monotone Funktionen beschränkte Klasse von Abhängigkeiten, die von ihnen wiedergegeben werden und durch die Art der Sensoreigenschaften bestimmt werden.

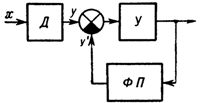
Reis. 2. Blockdiagramm der Linearisierung basierend auf dem Tracking-System: D – Sensor, U – Verstärker (Wandler), FP – Funktionswandler.

Linearisierer können nach folgenden Kriterien klassifiziert werden:

1. Nach der Methode zur Einstellung der Funktion: räumlich in Form von Vorlagen, Matrizen usw., in Form einer Kombination nichtlinearer Elemente, in Form eines digitalen Berechnungsalgorithmus, Geräten.

2.Nach dem Grad der Flexibilität des Schemas: universell (dh rekonfigurierbar) und spezialisiert.

3. Aufgrund der Art des Strukturdiagramms: offener (Abb. 1) und Kompensationstyp (Abb. 2).

4. In Form von Ein- und Ausgangswerten: analog, digital, gemischt (analog-digital und digital-analog).

5. Nach Art der im Stromkreis verwendeten Elemente: mechanisch, elektromechanisch, magnetisch, elektronisch usw.

Linearisierer für räumliche Funktionen umfassen hauptsächlich Nockenmechanismen, Muster und nichtlineare Potentiometer. Sie werden dort eingesetzt, wo der Messwert jeder Umwandlungsstufe in Form einer mechanischen Bewegung dargestellt wird (Nocken – zur Linearisierung der Eigenschaften von Manometer- und Transformatorsensoren, Modelle – in Schreibern, nichtlineare Potentiometer – in Potential- und Brückenschaltungen). ).

Die Nichtlinearität der Potentiometer-Kennlinien wird durch Aufwickeln auf Profilrahmen und Abschnitte mit der Methode der stückweisen linearen Näherung durch Manövrieren der Abschnitte mit geeigneten Widerständen erreicht.

Bei einem Linearisierer, der auf einem elektromechanischen Servosystem vom potentiometrischen Typ mit einem nichtlinearen Potentiometer basiert (Abb. 3), erscheint der linearisierte Wert als Drehwinkel oder mechanische Verschiebung. Diese Linearisierer sind einfach, vielseitig und werden häufig in zentralen Steuerungssystemen eingesetzt.

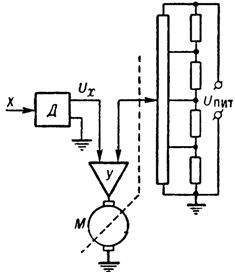
Reis. 3. Linearisierer für elektromechanisches Servosystem vom potentiometrischen Typ: D – Sensor mit Ausgang in Form einer Gleichspannung, Y – Verstärker, M – Elektromotor.

Nichtlinearitäten der Eigenschaften einzelner Elemente (elektronisch, magnetisch, thermisch usw.) werden in parametrischen Funktionswandlern genutzt. Eine vollständige Übereinstimmung zwischen den dabei entstehenden funktionalen Abhängigkeiten und den Eigenschaften der Sensoren lässt sich jedoch meist nicht erreichen.

Die algorithmische Art der Funktionseinstellung wird in digitalen Funktionskonvertern verwendet. Ihre Vorteile sind eine hohe Genauigkeit und Stabilität der Eigenschaften. Sie nutzen die mathematischen Eigenschaften einzelner funktionaler Abhängigkeiten oder das Prinzip der linearen Approximation durch Teile. Beispielsweise wird eine Parabel basierend auf den Eigenschaften von Quadraten ganzer Zahlen entwickelt.

Beispielsweise basiert ein digitaler Linearisierer auf der Methode der stückweisen linearen Näherung, die auf dem Prinzip basiert, die ankommenden Segmente mit Impulsen unterschiedlicher Wiederholfrequenz zu füllen. Die Füllfrequenzen ändern sich sprunghaft an den Grenzpunkten der sich nähernden Segmente entsprechend dem in das Gerät eingefügten Programm entsprechend der Art der Nichtlinearität. Die linearisierte Größe wird dann in einen Einheitscode umgewandelt.

Eine teilweise lineare Approximation der Nichtlinearität kann auch mit einem digitalen linearen Interpolator durchgeführt werden. In diesem Fall bleiben die Füllhäufigkeiten der Interpolationsintervalle nur im Mittel konstant.

Die Vorteile digitaler Linearisierer, die auf der Methode der linearen Approximation von Teilen basieren, sind: einfache Rekonfiguration der akkumulierten Nichtlinearität und die Geschwindigkeit des Umschaltens von einer Nichtlinearität zur anderen, was besonders in zentralen Hochgeschwindigkeitssteuerungssystemen wichtig ist.

In komplexen Steuerungssystemen mit Universalrechnern und Maschinen kann die Linearisierung direkt von diesen Maschinen aus durchgeführt werden, indem die Funktion in Form eines entsprechenden Unterprogramms eingebettet wird.