Resonanz von Strömen

Parallelschaltung eines Kondensators und einer Induktivität in einem Wechselstromkreis

Betrachten Sie die Phänomene in der Kette WechselstromEnthält einen Generator, einen Kondensator und eine Induktivität, die parallel geschaltet sind. Gehen Sie davon aus, dass der Stromkreis keinen aktiven Widerstand hat.

Offensichtlich ist in einem solchen Stromkreis die Spannung sowohl der Spule als auch des Kondensators zu jedem Zeitpunkt gleich der vom Generator erzeugten Spannung.

Der Gesamtstrom in einem Stromkreis besteht aus den Strömen in seinen Zweigen. Der Strom im induktiven Zweig eilt der Spannung in der Phase um ein Viertel der Periode nach, und der Strom im kapazitiven Zweig eilt ihr um das gleiche Viertel der Periode voraus. Daher erweisen sich die Ströme in den Zweigen zu jedem Zeitpunkt als um eine halbe Periode zueinander phasenverschoben, das heißt, sie sind gegenphasig. Somit sind die Ströme in den Zweigen jederzeit aufeinander gerichtet und der Gesamtstrom im unverzweigten Teil des Stromkreises entspricht ihrer Differenz.

Dies gibt uns das Recht, die Gleichheit I = IL -Integralschaltung zu schreiben

wo ich- Effektivwert des Gesamtstroms im Stromkreis, I L und integrierte Schaltung – Effektivwerte der Ströme in den Zweigen.

Unter Verwendung des Ohmschen Gesetzes zur Bestimmung der Effektivwerte des Stroms in den Zweigen erhalten wir:

Il = U / XL und Az° C = U / XC

Wenn der Stromkreis von induktivem Widerstand dominiert wird, d. h. XL Mehr ▼ XC, der Strom in der Spule ist geringer als der Strom im Kondensator; Daher ist der Strom im unverzweigten Abschnitt des Stromkreises kapazitiver Natur und der Stromkreis als Ganzes für den Generator ist kapazitiv. Umgekehrt ist bei XC größer als XL der Strom im Kondensator kleiner als der Strom in der Spule; Daher ist der Strom im unverzweigten Abschnitt des Stromkreises induktiv, und der Stromkreis für den Generator als Ganzes ist induktiv.

Es darf nicht vergessen werden, dass die Last in beiden Fällen reaktiv ist, d. h. Der Stromkreis verbraucht nicht den Strom des Generators.

Resonanz von Strömen

Betrachten wir nun den Fall, dass sich herausstellte, dass der parallel geschaltete Kondensator und die Spule in ihrer Reaktanz gleich sind, d.h. XlL = X°C.

Wenn wir wie zuvor davon ausgehen, dass die Spule und der Kondensator keinen aktiven Widerstand haben, dann ist bei gleichen Reaktionen (YL = Y° C) der Gesamtstrom im unverzweigten Teil des Stromkreises Null, während er in den Zweigen gleich ist Ströme werden mit größter Stärke fließen. In diesem Fall tritt im Stromkreis das Phänomen der Resonanzströme auf.

Bei Stromresonanz sind die Effektivwerte der Ströme in jedem Zweig, bestimmt durch die Verhältnisse IL = U / XL und Аz° С = U / XC, einander gleich, so dass XL = XC.

Die Schlussfolgerung, zu der wir gekommen sind, mag auf den ersten Blick etwas seltsam erscheinen. Tatsächlich ist der Generator mit zwei Widerständen belastet und im unverzweigten Teil des Stromkreises fließt kein Strom, während in den Widerständen selbst gleiche und darüber hinaus die größten Ströme fließen.

Dies erklärt sich aus dem Verhalten des Magnetfeldes der Spule und elektrisches Feld eines Kondensators… Bei Resonanz von Strömen, wie in SpannungsresonanzEs gibt eine Energieschwankung zwischen dem Feld der Spule und dem Feld des Kondensators. Nachdem der Generator die Energie an den Stromkreis weitergeleitet hat, scheint er isoliert zu sein. Es kann vollständig abgeschaltet werden und der Strom im verzweigten Teil des Stromkreises wird ohne Generator durch die Energie aufrechterhalten, die der Stromkreis zunächst speichert. Außerdem bleibt die Spannung an den Stromkreisklemmen genau die gleiche wie die vom Generator erzeugte.

Wenn wir also die Induktivität und den Kondensator parallel schalten, erhalten wir eine Oszillatorschaltung, die sich von der oben beschriebenen nur dadurch unterscheidet, dass der Generator, der die Schwingungen erzeugt, nicht direkt mit der Schaltung verbunden ist und die Schaltung geschlossen ist. 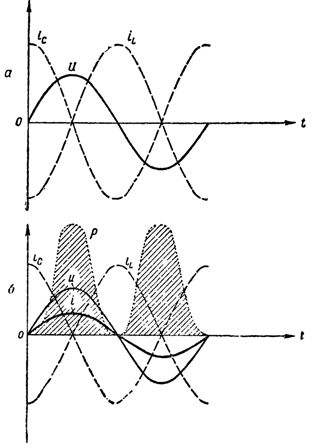Diagramme von Strömen, Spannung und Leistung im Stromkreis bei Resonanz der Ströme: a – der aktive Widerstand ist gleich Null, der Stromkreis verbraucht keine Energie; b – der Stromkreis hat einen aktiven Widerstand, im unverzweigten Teil des Stromkreises ist ein Strom aufgetreten, der Stromkreis verbraucht Energie

L, C und e, bei denen Stromresonanz auftritt, werden wie bei der Spannungsresonanz (wenn wir den aktiven Widerstand des Stromkreises vernachlässigen) durch die Gleichung bestimmt:

ωL = 1 / ω° C

Deshalb:

eres = 1 / 2π√LC

Lres = 1 / ω2C

Stück = 1 / ω2L

Durch Ändern einer dieser drei Größen kann die Gleichheit Xl = X° C erreicht werden, d. h. der Stromkreis wird in einen Schwingkreis umgewandelt.

Wir haben also einen geschlossenen Schwingkreis, in dem wir elektrische Schwingungen induzieren können, d. h. Wechselstrom. Und wenn es nicht den aktiven Widerstand gäbe, den jeder Schwingkreis besitzt, könnte in ihm ständig ein Wechselstrom existieren.Das Vorhandensein eines aktiven Widerstands führt dazu, dass die Schwingungen im Stromkreis allmählich nachlassen. Um sie aufrechtzuerhalten, ist eine Energiequelle erforderlich – ein Generator.

In nichtsinusförmigen Stromkreisen sind Resonanzmoden für verschiedene harmonische Komponenten möglich.

Resonanzströme werden in der Praxis häufig eingesetzt. Das Phänomen der Stromresonanz wird in Bandpassfiltern als elektrische „Klemme“ genutzt, die eine bestimmte Frequenz verzögert. Da bei der Frequenz f ein erheblicher Stromwiderstand vorhanden ist, ist der Spannungsabfall im Stromkreis bei der Frequenz f maximal. Diese Eigenschaft der Schleife wird Selektivität genannt und wird in Radioempfängern verwendet, um das Signal eines bestimmten Radiosenders zu isolieren. Eine der Hauptkomponenten ist ein Schwingkreis, der im resonanten Strommodus arbeitet elektronische Generatoren.