Verluste und Spannungsabfälle – was sind die Unterschiede?

Im normalen menschlichen Leben werden die Wörter „Verlust“ und „Sturz“ verwendet, um die Tatsache eines Rückgangs bestimmter Leistungen zu bezeichnen, sie bedeuten jedoch einen anderen Wert.

Unter „Verlusten“ versteht man in diesem Fall den Verlust eines Teils, eine Beschädigung oder eine Verkleinerung des zuvor erreichten Niveaus. Verluste sind unerwünscht, aber man kann sie tolerieren.

Unter dem Wort „Sturz“ wird ein schwerwiegenderer Schaden verstanden, der mit einer völligen Entrechtung verbunden ist. So können auch gelegentlich auftretende Verluste (z. B. eines Portfolios) im Laufe der Zeit zu einem Rückgang (z. B. der materiellen Lebensdauer) führen.

In diesem Zusammenhang werden wir diese Frage in Bezug auf die Spannung des Stromnetzes betrachten.

Wie Verluste und Spannungsabfälle entstehen

Der Strom wird über weite Strecken durch Freileitungen von einem Umspannwerk zum anderen transportiert.

Freileitungen dienen der Übertragung der zulässigen Leistung und bestehen aus Metalldrähten eines bestimmten Materials und Querschnitts. Sie erzeugen eine ohmsche Last mit einem Widerstandswert von R und einer Blindlast von X.

Auf der Empfangsseite steht es TransformatorStromumwandlung.Seine Spulen verfügen über einen aktiven und ausgeprägten induktiven Widerstand XL. Die Sekundärseite des Transformators senkt die Spannung und gibt sie an die Verbraucher weiter, deren Belastung durch den Wert Z ausgedrückt wird und aktiver, kapazitiver und induktiver Natur ist. Dies wirkt sich auch auf die elektrischen Parameter des Netzwerks aus.

Die Spannung, die an die Drähte der Stütze der Freileitung angelegt wird, die dem Umspannwerk am nächsten liegt, überwindet den Blind- und Wirkwiderstand des Stromkreises in jeder Phase und erzeugt darin einen Strom, dessen Vektor vom Vektor des Stromkreises abweicht angelegte Spannung um einen Winkel φ.

Die Art der Spannungsverteilung und des Stromflusses entlang der Leitung für einen symmetrischen Lastmodus ist auf dem Foto dargestellt.

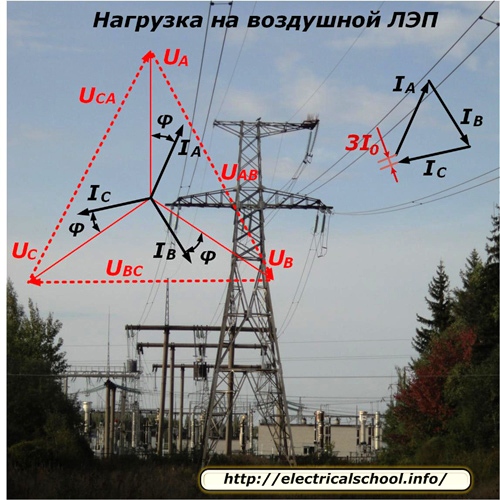
Da jede Phase der Leitung eine unterschiedliche Anzahl an Verbrauchern speist, die zudem zufällig vom Netz getrennt oder an den Betrieb angeschlossen werden, ist es technisch sehr schwierig, die Phasenbelastung perfekt auszugleichen. Darin herrscht immer ein Ungleichgewicht, das durch die vektorielle Addition der Phasenströme ermittelt und als 3I0 geschrieben wird. In den meisten Berechnungen wird es einfach ignoriert.

Die von der sendenden Umspannstation verbrauchte Energie wird teilweise für die Überwindung des Leitungswiderstands aufgewendet und erreicht die Empfangsseite kaum verändert. Dieser Anteil ist durch Verlust und Spannungsabfall gekennzeichnet, dessen Vektor in der Amplitude leicht abnimmt und in jeder Phase um einen Winkel verschoben wird.

So werden Verluste und Spannungsabfall berechnet

Um die Prozesse zu verstehen, die bei der Übertragung von Elektrizität ablaufen, eignet sich die Vektorform zur Darstellung der Hauptmerkmale. Auf dieser Methode basieren auch verschiedene mathematische Berechnungsverfahren.

Um die Berechnungen zu vereinfachen Dreiphasensystem es wird durch drei einphasige Ersatzschaltbilder dargestellt. Diese Methode funktioniert gut bei einer symmetrischen Last und ermöglicht die Analyse der Prozesse, wenn diese unterbrochen ist.

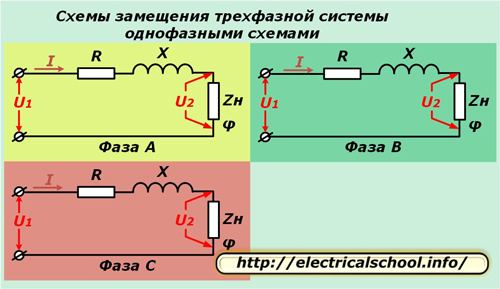
In den obigen Diagrammen sind der aktive Widerstand R und die Reaktanz X jedes Leiters der Leitung in Reihe mit dem komplexen Lastwiderstand Zn geschaltet, der durch den Winkel φ gekennzeichnet ist.

Darüber hinaus wird eine Berechnung des Spannungsverlusts und Spannungsabfalls in einer Phase durchgeführt. Dazu müssen Sie die Daten angeben. Hierzu wird eine Umspannstation ausgewählt, die Energie erhält, wobei bereits die zulässige Belastung ermittelt werden muss.

Der Spannungswert eines jeden Hochspannungssystems ist bereits in den Nachschlagewerken angegeben und die Widerstände der Drähte werden durch deren Länge, Querschnitt, Material und Konfiguration des Netzes bestimmt. Der maximale Strom im Stromkreis wird durch die Eigenschaften der Drähte eingestellt und begrenzt.

Um mit den Berechnungen zu beginnen, haben wir daher: U2, R, X, Z, I, φ.

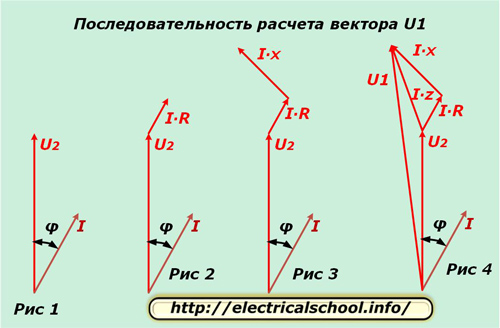
Wir nehmen eine Phase, zum Beispiel „A“, und trennen für sie in der komplexen Ebene die um einen Winkel φ verschobenen Vektoren U2 und I, wie in Abbildung 1 dargestellt. Die Potentialdifferenz im aktiven Widerstand des Leiters stimmt in der Richtung überein mit dem Strom und in der Größe wird aus dem Ausdruck I ∙ R bestimmt. Wir verschieben diesen Vektor vom Ende von U2 (Abb. 2).

Die Potentialdifferenz in der Reaktanz des Leiters unterscheidet sich von der Stromrichtung um einen Winkel φ1 und berechnet sich aus dem Produkt I ∙ X. Wir verschieben es aus dem Vektor I ∙ R (Abb. 3).

Zur Erinnerung: Für die positive Drehrichtung der Vektoren in der komplexen Ebene wird die Bewegung gegen den Uhrzeigersinn angenommen. Der durch die induktive Last fließende Strom eilt der angelegten Spannung um einen Winkel nach.

Abbildung 4 zeigt die Auftragung der Potentialdifferenzvektoren über den Gesamtdrahtwiderstand I ∙ Z und die Spannung am Eingang der Schaltung U1.

Jetzt können Sie die Eingangsvektoren mit der Ersatzschaltung und über die Last hinweg vergleichen. Legen Sie dazu das resultierende Diagramm horizontal (Abb. 5) und zeichnen Sie von Anfang an einen Bogen mit dem Radius des Moduls U1, bis er die Richtung des Vektors U2 schneidet (Abb. 6).

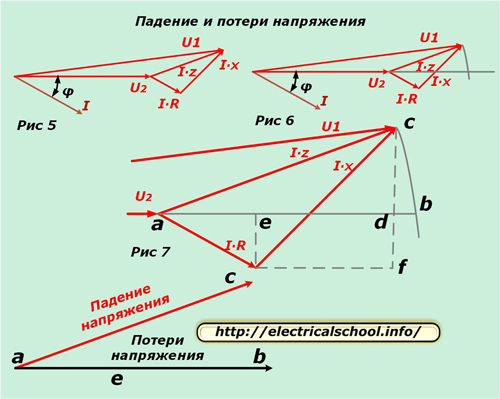
Abbildung 7 zeigt eine Vergrößerung des Dreiecks zur besseren Übersichtlichkeit und die Einzeichnung von Hilfslinien, die die charakteristischen Schnittpunkte mit Buchstaben markieren.

Unten im Bild ist zu sehen, dass der resultierende Vektor ac als Spannungsabfall und ab als Verlust bezeichnet wird. Sie unterscheiden sich in Größe und Richtung. Wenn wir zum ursprünglichen Maßstab zurückkehren, werden wir sehen, dass ac als Ergebnis der geometrischen Subtraktion von Vektoren (U2 von U1) erhalten wird und ab arithmetisch ist. Dieser Vorgang ist im Bild unten dargestellt (Abb. 8).

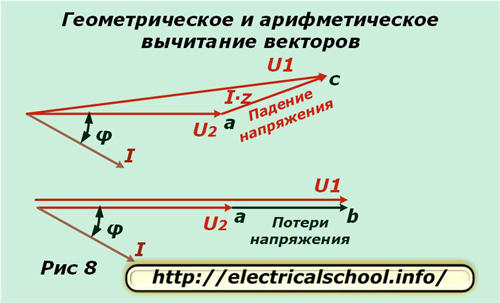
Herleitung von Formeln zur Berechnung von Spannungsverlusten

Kehren wir nun zu Abbildung 7 zurück und stellen fest, dass das BD-Segment sehr klein ist. Aus diesem Grund wird er in den Berechnungen vernachlässigt und der Spannungsverlust aus der Segmentlänge ad berechnet. Sie besteht aus zwei Liniensegmenten ae und ed.

Da ae = I ∙ R ∙ cosφ und ed = I ∙ x ∙ sinφ ist, kann der Spannungsverlust für eine Phase mit der Formel berechnet werden:

∆Uph = I ∙ R ∙ cosφ + I ∙ x ∙ sinφ

Wenn wir davon ausgehen, dass die Last in allen Phasen symmetrisch ist (bedingte Vernachlässigung von 3I0), können wir mit mathematischen Methoden den Spannungsverlust in der Leitung berechnen.

∆Ul = √3I ∙ (R ∙ cosφ + x ∙ sinφ)

Wenn die rechte Seite dieser Formel mit der Netzspannung Un multipliziert und dividiert wird, erhalten wir eine Formel, mit der wir die Spannungsverluste durch die Stromversorgung p berechnen können.

∆Ul = (P ∙ r + Q ∙ x) / Un

Die Werte der Wirkleistung P und der Blindleistung Q können den Ablesungen der Leitungszähler entnommen werden.

Somit hängt der Spannungsverlust in einem Stromkreis ab von:

• Aktiv- und Reaktanz des Stromkreises;

• Komponenten der angewandten Leistung;

• die Größe der angelegten Spannung.

Herleitung von Formeln zur Berechnung der Querkomponente des Spannungsabfalls

Kehren wir zu Abbildung 7 zurück. Der Wert des Vektors ac kann durch die Hypotenuse eines rechtwinkligen Dreiecks acd dargestellt werden. Den Anzeigenfuß haben wir bereits berechnet. Bestimmen wir die Querkomponente cd.

Die Abbildung zeigt, dass cd = cf-df.

df = ce = I ∙ R ∙ sin φ.

cf = I ∙ x ∙ cos φ.

cd = I ∙ x ∙ cosφ-I ∙ R ∙ sinφ.

Mithilfe der erhaltenen Modelle führen wir kleine mathematische Transformationen durch und ermitteln die Querkomponente des Spannungsabfalls.

δU = √3I ∙ (x ∙ cosφ-r ∙ sinφ) = (P ∙ x-Q ∙ r) / Un.

Bestimmung der Formel zur Berechnung der Spannung U1 am Anfang der Stromleitung

Wenn wir den Wert der Spannung am Ende der Leitung U2, den Verlust ∆Ul und die Querkomponente des Abfalls δU kennen, können wir den Wert des Vektors U1 nach dem Satz des Pythagoras berechnen. In erweiterter Form hat es die folgende Form.

U1 = √ [(U2 + (Pr + Qx) / Un)2+ ((Px-Qr) / Un)2].

Praktischer Nutzen

Die Berechnung der Spannungsverluste wird von Ingenieuren in der Phase der Erstellung eines Stromkreisprojekts durchgeführt, um die Konfiguration des Netzwerks und seiner Bestandteile optimal auszuwählen.

Während des Betriebs elektrischer Anlagen können bei Bedarf in regelmäßigen Abständen gleichzeitige Messungen der Spannungsvektoren an den Leitungsenden durchgeführt und die mit der Methode einfacher Berechnungen erzielten Ergebnisse verglichen werden. Diese Methode eignet sich für Geräte, die gewachsen sind Anforderungen aufgrund der Notwendigkeit einer hohen Arbeitsgenauigkeit.

Spannungsverluste in Sekundärkreisen

Ein Beispiel sind die Sekundärkreise von Messspannungswandlern, die teilweise mehrere hundert Meter lang sind und über ein spezielles Stromkabel mit erhöhtem Querschnitt übertragen werden.

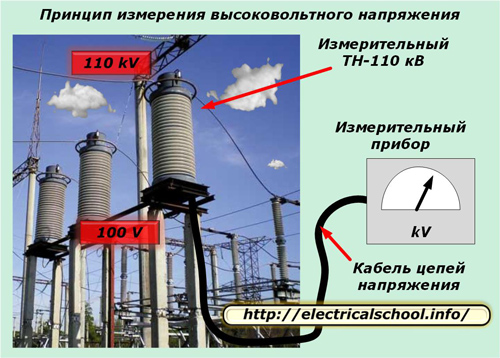
An die elektrischen Eigenschaften eines solchen Kabels werden erhöhte Anforderungen an die Qualität der Spannungsübertragung gestellt.

Der moderne Schutz elektrischer Geräte erfordert den Betrieb von Messsystemen mit hohen messtechnischen Indikatoren und einer Genauigkeitsklasse von 0,5 oder sogar 0,2. Daher müssen Verluste der an ihnen anliegenden Spannung überwacht und berücksichtigt werden. Andernfalls kann der von ihnen in den Betrieb des Geräts eingeführte Fehler alle Betriebseigenschaften erheblich beeinträchtigen.

Spannungsverluste in langen Kabelstrecken

Die Besonderheit des Designs des langen Kabels besteht darin, dass es aufgrund der relativ engen Anordnung der leitenden Adern und einer dünnen Isolationsschicht dazwischen einen kapazitiven Widerstand aufweist. Es lenkt den durch das Kabel fließenden Stromvektor weiter ab und verändert seine Größe.

Der Einfluss des Spannungsabfalls auf den kapazitiven Widerstand muss bei der Berechnung berücksichtigt werden, um den Wert von I ∙ z zu ändern. Ansonsten ändert sich an der oben beschriebenen Technologie nichts.

Der Artikel liefert Beispiele für Verluste und Spannungsabfälle an Freileitungen und Kabeln. Sie finden sich jedoch in allen Stromverbrauchern, einschließlich Elektromotoren, Transformatoren, Induktoren, Kondensatorbatterien und anderen Geräten.

Die Höhe der Spannungsverluste ist für jede Art von Elektrogeräten in Bezug auf die Betriebsbedingungen gesetzlich geregelt und das Prinzip ihrer Ermittlung ist in allen Stromkreisen gleich.