Heizung und Kühlung von Elektromotoren
 Die korrekte Bestimmung der Leistung von Elektromotoren für verschiedene Metallschneidemaschinen, -mechanismen und -maschinen ist von großer Bedeutung. Bei unzureichender Leistung ist es unmöglich, die Produktionskapazitäten der Maschine vollständig zu nutzen und den geplanten technologischen Prozess durchzuführen. Reicht die Leistung nicht aus, fällt der Elektromotor vorzeitig aus.
Die korrekte Bestimmung der Leistung von Elektromotoren für verschiedene Metallschneidemaschinen, -mechanismen und -maschinen ist von großer Bedeutung. Bei unzureichender Leistung ist es unmöglich, die Produktionskapazitäten der Maschine vollständig zu nutzen und den geplanten technologischen Prozess durchzuführen. Reicht die Leistung nicht aus, fällt der Elektromotor vorzeitig aus.
Eine Überschätzung der Leistung des Elektromotors führt zu einer systematischen Unterladung und damit zu einer unvollständigen Nutzung des Motors, seinem Betrieb mit geringem Wirkungsgrad und einem kleinen Leistungsfaktor (bei Asynchronmotoren). Wenn die Motorleistung überbewertet wird, steigen außerdem die Kapital- und Betriebskosten.
Die zum Betrieb der Maschine erforderliche Leistung und damit die vom Elektromotor entwickelte Leistung ändert sich während des Maschinenbetriebs. Die Belastung eines Elektromotors kann durch das Belastungsdiagramm (Abb. 1) charakterisiert werden, das die Abhängigkeit der Leistung von der Motorwelle, ihres Drehmoments oder Stroms von der Zeit darstellt.Nach Abschluss der Bearbeitung des Werkstücks wird die Maschine angehalten, das Werkstück vermessen und das Werkstück ausgewechselt. Anschließend wiederholt sich der Ladeplan noch einmal (bei der Bearbeitung gleichartiger Teile).
Um den Normalbetrieb unter einer solchen variablen Belastung zu gewährleisten, muss der Elektromotor während der Bearbeitung die höchste erforderliche Leistung entwickeln und darf im Dauerbetrieb gemäß diesem Belastungsplan nicht überhitzen. Die zulässige Überlastung von Elektromotoren wird durch deren elektrische Eigenschaften bestimmt.

Reis. 1. Laden Sie den Plan, wenn Sie Teile desselben Typs bearbeiten
Wenn der Motor läuft, Energieverluste (und Leistungsverluste).wodurch es sich erwärmt. Ein Teil der vom Elektromotor verbrauchten Energie wird für die Erwärmung seiner Wicklungen und für die Erwärmung des Magnetkreises aufgewendet Hysterese und Wirbelströme mit Reibung und Luftreibung. Die Wärmeverluste der Wicklungen, proportional zum Quadrat des Stroms, werden als variabel bezeichnet (ΔРtrans)... Die verbleibenden Verluste im Motor hängen ein wenig von seiner Belastung ab und werden herkömmlicherweise als Konstanten (ΔРpos) bezeichnet.
Die zulässige Erwärmung eines Elektromotors wird durch die am wenigsten hitzebeständigen Materialien seiner Konstruktion bestimmt. Dieses Material ist die Isolierung seiner Spule.
Zur Isolierung elektrischer Maschinen werden verwendet:
• Baumwoll- und Seidenstoffe, Garne, Papier und faserige organische Materialien, die nicht mit isolierenden Verbindungen imprägniert sind (Hitzebeständigkeitsklasse U);
• die gleichen Materialien, imprägniert (Klasse A);
• synthetische organische Filme (Klasse E);
• Materialien aus Asbest, Glimmer, Glasfaser mit organischen Bindemitteln (Klasse B);
• das gleiche, jedoch mit synthetischen Bindemitteln und Imprägniermitteln (Klasse F);
• die gleichen Materialien, jedoch mit Silikonbindemitteln und Imprägniermitteln (Klasse H);
• Glimmer, Keramik, Glas, Quarz ohne Bindemittel oder mit anorganischen Bindemitteln (Klasse C).
Die Isolationsklassen U, A, E, B, F, H erlauben jeweils maximale Temperaturen von 90, 105, 120, 130, 155, 180 °C. Die Grenztemperatur der Klasse C übersteigt 180 °C und wird durch die Eigenschaften der Isolierung begrenzt verwendete Materialien.
Bei gleicher Belastung des Elektromotors ist dessen Erwärmung bei unterschiedlichen Umgebungstemperaturen ungleichmäßig. Die Auslegungstemperatur t0 der Umgebung beträgt 40 °C. Bei dieser Temperatur werden die Nennleistungswerte der Elektromotoren ermittelt. Der Anstieg der Temperatur des Elektromotors über die Umgebungstemperatur wird als Überhitzung bezeichnet:
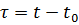
Der Einsatz synthetischer Dämmstoffe nimmt zu. Insbesondere Silizium-Silizium-Isolierungen gewährleisten eine hohe Zuverlässigkeit elektrischer Maschinen beim Betrieb unter tropischen Bedingungen.
Die in verschiedenen Teilen des Motors erzeugte Wärme wirkt sich unterschiedlich stark auf die Erwärmung der Isolierung aus. Darüber hinaus findet zwischen den einzelnen Teilen des Elektromotors ein Wärmeaustausch statt, dessen Art sich je nach Belastungszustand ändert.
Die unterschiedliche Erwärmung der einzelnen Teile des Elektromotors und die Wärmeübertragung zwischen ihnen erschwert die analytische Untersuchung des Prozesses. Daher wird der Einfachheit halber bedingt davon ausgegangen, dass der Elektromotor ein thermisch homogener und unendlich wärmeleitender Körper ist. Es wird allgemein angenommen, dass die von einem Elektromotor an die Umgebung abgegebene Wärme proportional zur Überhitzung ist.In diesem Fall wird die Wärmestrahlung vernachlässigt, da die absoluten Erwärmungstemperaturen der Motoren niedrig sind. Betrachten Sie den Aufheizvorgang des Elektromotors unter den gegebenen Annahmen.
Beim Arbeiten im Elektromotor wird während der Zeit dt die Wärme dq abgegeben. Ein Teil dieser Wärme dq1 wird von der Masse des Elektromotors aufgenommen, wodurch die Temperatur t und die Überhitzung τ des Motors ansteigen. Die verbleibende Wärme dq2 wird vom Motor an die Umgebung abgegeben. Somit kann die Gleichheit geschrieben werden
Mit steigender Motortemperatur steigt die Wärme dq2. Ab einem bestimmten Überhitzungswert wird so viel Wärme an die Umgebung abgegeben, wie im Elektromotor abgegeben wird; dann gilt dq = dq2 und dq1 = 0. Die Temperatur des Elektromotors steigt nicht mehr an und die Überhitzung erreicht einen stationären Wert von τу.
Unter den oben genannten Annahmen kann die Gleichung wie folgt geschrieben werden:
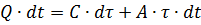
wobei Q die Wärmeleistung aufgrund von Verlusten im Elektromotor ist, J/s; A – Wärmeübertragung vom Motor, d. h. die Wärmemenge, die der Motor pro Zeiteinheit bei einem Temperaturunterschied zwischen Motor und Umgebung von 1 °C, J/s-Grad, an die Umgebung abgibt; C ist die Wärmekapazität des Motors, d.h. die Wärmemenge, die erforderlich ist, um die Temperatur des Motors um 1 °C, J/Grad, zu erhöhen.
Wenn wir die Variablen in der Gleichung trennen, haben wir
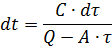
Wir integrieren die linke Seite der Gleichung im Bereich von Null bis zu einem aktuellen Wert der Zeit t und die rechte Seite im Bereich von der anfänglichen Überhitzung τ0 des Elektromotors bis zum aktuellen Überhitzungswert τ:
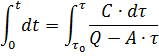
Wenn wir die Gleichung nach τ auflösen, erhalten wir eine Gleichung für die Erwärmung eines Elektromotors:
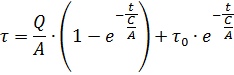
Bezeichnen wir C / A = T und bestimmen wir die Dimension dieses Verhältnisses:
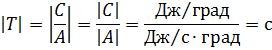
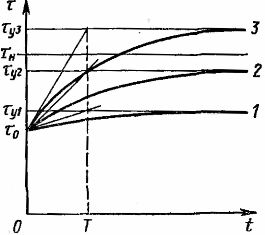
Reis. 2. Kurven, die die Erwärmung des Elektromotors charakterisieren
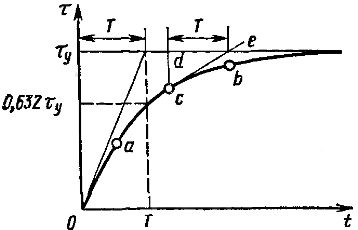
Reis. 3. Bestimmung der Heizzeitkonstante
Man nennt sie die Größe T, die die Dimension Zeitkonstante der Aufheizzeit des Elektromotors hat. In Übereinstimmung mit dieser Notation kann die Erwärmungsgleichung umgeschrieben werden als
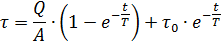
Wie Sie der Gleichung entnehmen können, erhalten wir den stationären Überhitzungswert.
Wenn sich die Belastung des Elektromotors ändert, ändert sich die Höhe der Verluste und damit der Wert von Q. Dies führt zu einer Änderung des Wertes von τу.
In Abb. In Fig. 2 sind die der letzten Gleichung entsprechenden Heizkurven 1, 2, 3 für unterschiedliche Belastungswerte dargestellt. Wenn τу den Wert der zulässigen Überhitzung τn überschreitet, ist der Dauerbetrieb des Elektromotors nicht akzeptabel. Wie aus der Gleichung und den Diagrammen (Abb. 2) hervorgeht, ist der Anstieg der Überhitzung asymptotisch.
Wenn wir den Wert t = 3T in die Gleichung einsetzen, erhalten wir einen Wert von τ, der etwa nur 5 % kleiner als τy ist. Somit kann während der Zeit t = 3T der Aufheizvorgang praktisch als abgeschlossen betrachtet werden.
Wenn Sie an irgendeinem Punkt der Heizkurve (Abb. 3) eine Tangente an die Heizkurve zeichnen, dann eine Vertikale durch denselben Punkt zeichnen, dann das Segment de der Asymptote, geschlossen zwischen der Tangente und der Vertikalen, auf der Skala der Abszissenachse ist gleich T. Wenn wir Q = 0 in die Gleichung aufnehmen, erhalten wir die Motorkühlungsgleichung:
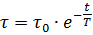
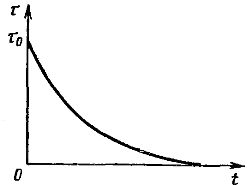
Die Abkühlungskurve in Abb. 4, entspricht dieser Gleichung.
Die Zeitkonstante der Erwärmung wird durch die Größe des Elektromotors und die Art seines Schutzes vor Umwelteinflüssen bestimmt. Bei offenen und geschützten Elektromotoren mit geringer Leistung beträgt die Aufheizzeit 20-30 Minuten. Bei geschlossenen Hochleistungselektromotoren beträgt sie 2-3 Stunden.
Wie oben erwähnt, ist die angegebene Theorie der Erwärmung von Elektromotoren Näherungswerte und basiert auf groben Annahmen. Daher weicht die experimentell gemessene Aufheizkurve deutlich von der theoretischen ab. Wenn für verschiedene Punkte der experimentellen Heizkurve die in Abb. 3 zeigt sich, dass die Werte von T mit zunehmender Zeit zunehmen. Daher sollten alle nach der Gleichung durchgeführten Berechnungen als Näherungswerte betrachtet werden. Bei diesen Berechnungen empfiehlt es sich, die grafisch ermittelte Konstante T für den Startpunkt der Heizkurve zu verwenden. Dieser Wert von T ist der kleinste und bietet bei Verwendung einen gewissen Spielraum für die Motorleistung.
Reis. 4. Motorkühlkurve
Die experimentell gemessene Abkühlkurve weicht noch stärker von der theoretischen ab als die Aufheizkurve. Die Abkühlzeitkonstante entsprechend dem ausgeschalteten Motor ist aufgrund der verringerten Wärmeübertragung bei fehlender Belüftung deutlich länger als die Heizzeitkonstante.