Bestimmung der Motorleistung im repetitiven Übergangsbetrieb
 Die Betriebsweise des Elektroantriebs, bei der die Betriebsperioden so lang sind und sich mit Pausen von bestimmter Dauer abwechseln, dass die Temperatur aller Geräte, aus denen der Elektroantrieb besteht, keinen stabilen Wert erreicht, Weder während jeder Arbeitsperiode noch während jeder Pause wird eine Unterbrechung aufgerufen.
Die Betriebsweise des Elektroantriebs, bei der die Betriebsperioden so lang sind und sich mit Pausen von bestimmter Dauer abwechseln, dass die Temperatur aller Geräte, aus denen der Elektroantrieb besteht, keinen stabilen Wert erreicht, Weder während jeder Arbeitsperiode noch während jeder Pause wird eine Unterbrechung aufgerufen.
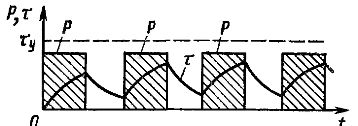
Das periodische Belastungsregime entspricht Diagrammen, die denen in Abb. ähneln. 1. Die Überhitzung des Elektromotors variiert entlang der gestrichelten Linie einer Säge, die aus abwechselnden Segmenten von Heiz- und Kühlkurven besteht. Der intermittierende Lastmodus ist typisch für die meisten Werkzeugmaschinenantriebe.
Reis. 1. Intermittierender Lastplan
Die Leistung eines im periodischen Modus betriebenen Elektromotors lässt sich am einfachsten durch die Formel für durchschnittliche Verluste bestimmen, die wie folgt geschrieben werden kann
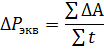
Dabei ist ΔA der Energieverlust bei jedem Lastwert, einschließlich der Start- und Stoppvorgänge.
Wenn der Elektromotor nicht läuft, verschlechtern sich die Kühlbedingungen deutlich. Dies wird durch die Einführung experimenteller Koeffizienten β0 <1 berücksichtigt. Die Pausenzeit t0 wird mit dem Koeffizienten β0 multipliziert, wodurch der Nenner der Formel kleiner wird und die äquivalenten Verluste ΔREKV zunehmen und dementsprechend die Nennleistung des Elektromotors steigt.
Für asynchrone geschützte Motoren der A-Serie mit einer Synchrondrehzahl von 1500 U/min und einer Leistung von 1-100 kW beträgt der β0-Koeffizient 0,50-0,17 und für Abschlämmmotoren β0 = 0,45-0,3 (mit einer Erhöhung von Пн , Koeffizient β0 nimmt ab). Bei geschlossenen Motoren liegt β0 nahe bei Eins (0,93–0,98). Dies liegt daran, dass die Belüftungseffizienz geschlossener Motoren gering ist.
Beim Starten und Stoppen liegt die Durchschnittsdrehzahl des Elektromotors unter der Nenndrehzahl, wodurch sich auch die Kühlung des Elektromotors verschlechtert, was durch den Koeffizienten charakterisiert wird

Bei der Bestimmung des Koeffizienten β1 wird bedingt angenommen, dass die Änderung der Rotationsfrequenz nach einem linearen Gesetz erfolgt und der Koeffizient β1 linear davon abhängt.
Wenn wir die Koeffizienten β0 und β1 kennen, erhalten wir
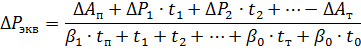
wobei ΔР1, ΔР2, — Leistungsverluste bei verschiedenen Lasten, kW; t1 t2 – Wirkungszeit dieser Lasten, s; tn, tT, t0 – Start-, Verzögerungs- und Pausenzeit, s; ΔАп ΔАТ – Energieverluste im Motor beim Starten und Stoppen, kJ.
Wie oben erwähnt, muss jeder Motor für Erwärmungs- und Überlastbedingungen ausgewählt werden. Um die Methode der durchschnittlichen Verluste anwenden zu können, ist es notwendig, im Voraus einen bestimmten Elektromotor einzurichten, dessen Auswahl auch in diesem Fall entsprechend den Überlastbedingungen empfohlen wird.Die Ersatzleistungsformel kann für eine grobe Berechnung in Fällen verwendet werden, in denen Starts und Stopps selten sind und die Erwärmung des Elektromotors nicht wesentlich beeinflussen.
Im Maschinenbau werden für den Betrieb im intermittierenden Lastbetrieb Elektromotoren eingesetzt, die für den Dauerlastbetrieb ausgelegt sind. Die Elektroindustrie produziert auch Motoren, die speziell für die Bewältigung intermittierender Lasten ausgelegt sind und häufig in Hebe- und Transportkonstruktionen eingesetzt werden. Solche Elektromotoren werden unter Berücksichtigung der relativen Einschaltdauer ausgewählt:

wobei tp die Motorlaufzeit ist; t0 – Pausendauer.
Ein Beispiel für die Auswahl eines Motors nach Leistung im Mehrfachkurzzeitbetriebsmodus.
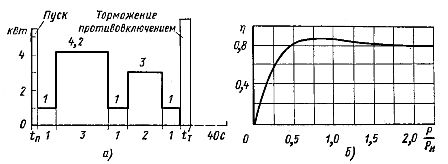
Bestimmen Sie die Leistung des Elektromotors bei n0 – 1500 U/min; Der Motor arbeitet gemäß dem in Abb. gezeigten Lastplan. 2, a. Wellenleistung des Elektromotors im Leerlauf der Maschine Pxx = 1 kW. Reduziertes Trägheitsmoment der Maschine Jc = 0,045 kg-m2.
Antworten:
1. Den Elektromotor entsprechend den Überlastbedingungen vorwählen, z. B. λ = 1,6:

Laut Katalog wählen wir einen Elektromotor mit der geschützten Version der nächsthöheren Leistung (2,8 kW), bei der mon = 1420 U/min;

Für diesen Motor gilt λ = 0,85 • 2 = 1,7. Auf diese Weise wird der Motor mit einer bestimmten Überlastgrenze ausgewählt.
Die Abhängigkeit η = f (P / Pн) dieses Motors ist in Abb. dargestellt. 2, geb.
Reis. 2. Abhängigkeiten N = f (t) und η = f (P / Pн)
2. Nach der Formel
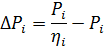
wir erkennen Verluste bei Potenzen 1; 3; 4,2 kW (planmäßig). Die Verluste betragen jeweils 0,35; 0,65 und 1 kW. Wir finden Verluste bei Pn = 2,8 kW, die ΔPn = 0,57 kW betragen.
3. Bestimmen Sie die Startzeit und die Stoppzeit durch Opposition:
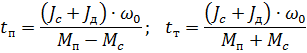
Wo:
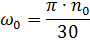
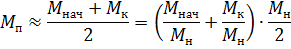



Wir erhalten tn = 0,30 s; tt = 0,21 s.
4. Bestimmen Sie die Start- und Stoppverluste:

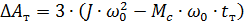
Wir erhalten ΔAp = 1,8 kJ und ΔAt = 3,8 kJ.
5. Finden Sie die äquivalenten Verluste in der Schleife:
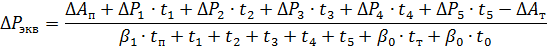
Wo
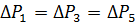
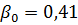
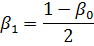
Wir erhalten ΔREKV = 0,44 kW. Da ΔPn = 0,57, gilt ΔREKV <ΔPn und daher ist der Motor richtig ausgewählt.