Was ist eine Stromversorgung?

Der moderne Mensch ist im Alltag und bei der Arbeit ständig mit Elektrizität konfrontiert, nutzt Geräte, die elektrischen Strom verbrauchen, und Geräte, die ihn erzeugen. Bei der Arbeit mit ihnen sollten Sie immer ihre inhärenten technischen Eigenschaften berücksichtigen.

Einer der Hauptindikatoren jedes elektrischen Geräts ist eine physikalische Größe wie elektrische Energie... Es ist üblich, die Intensität oder Geschwindigkeit der Erzeugung, Übertragung oder Umwandlung von Elektrizität in andere Energiearten zu bezeichnen, beispielsweise Wärme, Licht, mechanisch.

Der Transport oder die Übertragung großer elektrischer Energie für industrielle Zwecke erfolgt gem Hochspannungsleitungen.

Transformation elektrische Energie erfolgt in Umspannwerken.

Der Stromverbrauch erfolgt in Haushalts- und Industriegeräten für verschiedene Zwecke. Einer ihrer häufigsten Typen ist Glühlampen verschiedener Leistungsstufen.

Die elektrische Leistung von Generatoren, Stromleitungen und Verbrauchern in Gleich- und Wechselstromkreisen hat die gleiche physikalische Bedeutung, die sich je nach Form der zusammengesetzten Signale gleichzeitig in unterschiedlichen Verhältnissen ausdrückt. Um die allgemeinen Muster zu definieren, Vorstellungen von Momentanwerten... Sie betonen erneut die Abhängigkeit der Umwandlungsrate der Elektrizität von der Zeit.

Bestimmung der momentanen elektrischen Leistung

In der theoretischen Elektrotechnik werden zur Ableitung der grundlegenden Zusammenhänge zwischen Strom, Spannung und Leistung deren Abbilder in Form von Momentanwerten verwendet, die zu einem bestimmten Zeitpunkt feststehen.

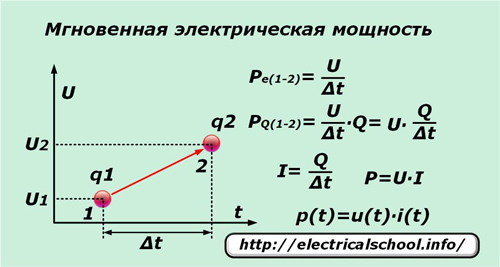
Wenn sich in einer sehr kurzen Zeitspanne ∆t eine einzelne Elementarladung q unter dem Einfluss der Spannung U vom Punkt „1“ zum Punkt „2“ bewegt, dann verrichtet sie Arbeit gleich der Potentialdifferenz zwischen diesen Punkten. Wenn wir es durch das Zeitintervall ∆t dividieren, erhalten wir den Ausdruck für die Momentanleistung pro Ladungseinheit Pe (1-2).

Da sich unter der Wirkung der angelegten Spannung nicht nur eine einzelne Ladung bewegt, sondern auch alle benachbarten Ladungen, die unter dem Einfluss dieser Kraft stehen, deren Anzahl zweckmäßigerweise durch die Zahl Q dargestellt wird, ist der Momentanwert der Leistung PQ (1-2) kann für sie geschrieben werden.

Nach Durchführung einfacher Transformationen erhalten wir den Ausdruck für die Leistung P und die Abhängigkeit ihres Momentanwerts p (t) von den Komponenten des Produkts aus Momentanstrom i (t) und Spannung u (t).

Bestimmung der konstanten elektrischen Leistung

V Gleichstromkreise Die Größe des Spannungsabfalls im Stromkreisabschnitt und der durch ihn fließende Strom ändern sich nicht und bleiben stabil, gleich den Momentanwerten.Daher kann die Leistung in dieser Schaltung bestimmt werden, indem man diese Werte multipliziert oder die perfekte Arbeit A durch den Zeitraum ihrer Ausführung dividiert, wie im erläuternden Bild gezeigt.

Bestimmung der elektrischen Wechselstromleistung

Die Gesetze der sinusförmigen Variation von Strömen und Spannungen, die über elektrische Netzwerke übertragen werden, üben ihren Einfluss auf die Leistungsausprägung in solchen Schaltkreisen aus. Hier kommt die Scheinleistung ins Spiel, die durch das Leistungsdreieck beschrieben wird und sich aus Wirk- und Blindanteilen zusammensetzt.

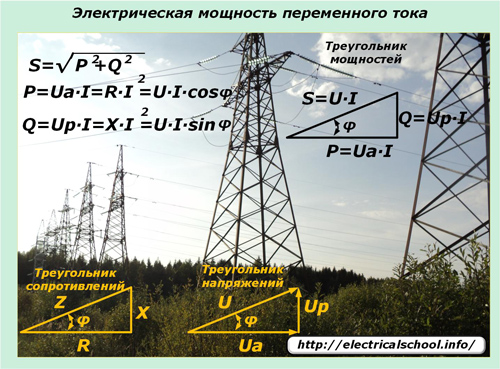
Ein sinusförmiger elektrischer Strom ändert beim Durchgang durch Stromleitungen mit gemischten Lasttypen in allen Abschnitten die Form seiner Harmonischen nicht. Und der Spannungsabfall bei Blindlasten verschiebt sich phasengleich in eine bestimmte Richtung. Momentwertausdrücke helfen dabei, die Auswirkung angelegter Lasten auf die Leistungsänderung im Stromkreis und deren Richtung zu verstehen.

Beachten Sie dabei sofort, dass die Richtung des Stromflusses vom Generator zum Verbraucher und die übertragene Leistung durch den erstellten Stromkreis völlig unterschiedliche Dinge sind, die in manchen Fällen nicht nur nicht übereinstimmen, sondern auch sein können in entgegengesetzte Richtungen gerichtet.

Betrachten Sie diese Zusammenhänge in ihrer idealen, reinen Ausprägung für verschiedene Belastungsarten:

• aktiv;

• kapazitiv;

• induktiv.

Verlustleistung der aktiven Last

Wir gehen davon aus, dass der Generator eine ideale Sinusspannung u erzeugt, die an den rein aktiven Widerstand des Stromkreises angelegt wird. Amperemeter A und Voltmeter V messen zu jedem Zeitpunkt t den Strom I und die Spannung U.

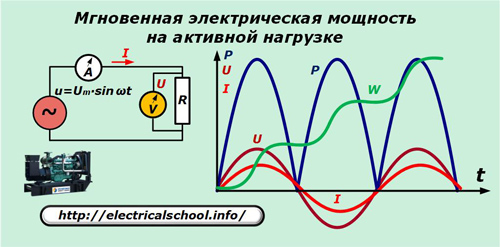
Die Grafik zeigt, dass die Sinuskurven des Stroms und des Spannungsabfalls am aktiven Widerstand in Frequenz und Phase übereinstimmen und die gleichen Schwingungen erzeugen. Die durch ihr Produkt ausgedrückte Kraft schwingt mit der doppelten Frequenz und bleibt immer positiv.

p = u ∙ i = Um ∙ sinωt ∙ Um / R ∙ sinωt = Um2/ R ∙ sin2ωt = Um2/ 2R ∙ (1-cos2ωt).

Wenn wir zum Ausdruck gehen Betriebsspannung, dann erhalten wir: p = P ∙ (1-cos2ωt).

Wir integrieren dann die Leistung über die Periode einer Schwingung T und können feststellen, dass der Energiegewinn ∆W während dieses Intervalls zunimmt. Im Laufe der Zeit verbraucht der Widerstand immer wieder neue Strommengen, wie in der Grafik dargestellt.

Bei reaktiven Lasten sind die Eigenschaften des Energieverbrauchs unterschiedlich, sie haben eine andere Form.

Kapazitive Verlustleistung

Ersetzen Sie im Stromkreis des Generators das Widerstandselement durch einen Kondensator mit der Kapazität C.

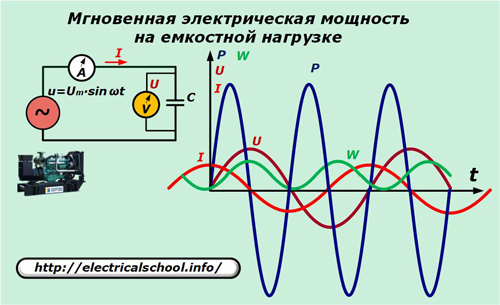
Der Zusammenhang zwischen dem Strom und dem Spannungsabfall in der Kapazität wird durch das Verhältnis ausgedrückt: I = C ∙ dU / dt = ω ∙ C ∙ Um ∙ cosωt.

Wir multiplizieren die Werte der Momentanausdrücke von Strom mit Spannung und erhalten den Wert der Leistung, die von der kapazitiven Last verbraucht wird.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Um ∙ cosωt = ω ∙ C ∙ Um2∙ sinωt ∙ cosωt = Um2/ (2X° C) ∙ sin2ωt = U2/ (2X° C) ∙ sin2ωt.

Hier sieht man, dass die Leistung mit der doppelten Frequenz der angelegten Spannung um Null schwankt. Sein Gesamtwert für die harmonische Periode sowie der Energiegewinn sind Null.

Das bedeutet, dass sich Energie entlang des geschlossenen Kreislaufs in beide Richtungen bewegt, aber keine Arbeit verrichtet.Diese Tatsache erklärt sich aus der Tatsache, dass die Leistung positiv ist und der Energiefluss durch den Stromkreis zum Behälter geleitet wird, wo die Energie akkumuliert wird, wenn die Spannung der Quelle im absoluten Wert ansteigt.

Nachdem die Spannung zum Abschnitt mit fallenden Oberwellen gelangt ist, wird Energie vom Kondensator zum Stromkreis zur Quelle zurückgeführt. In beiden Prozessen wird keine nützliche Arbeit geleistet.

Verlustleistung in einer induktiven Last

Ersetzen Sie nun im Versorgungskreis den Kondensator durch die Induktivität L.

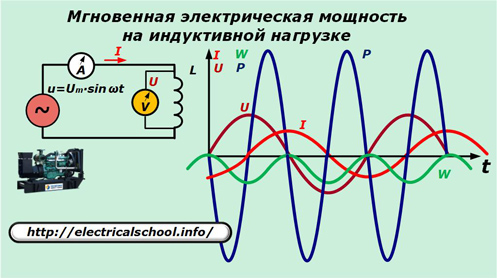
Hier wird der Strom durch die Induktivität durch das Verhältnis ausgedrückt:

I = 1 / L∫udt = -Um / ωL ∙ cos ωt.

Dann bekommen wir

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ (-Um / ωL ∙ cosωt) = — Um2/ ωL ∙ sinωt ∙ cosωt = -Um2/ (2ХL) ∙ sin2ωt = -U2/ (2ХL) ∙ sin2ωt.

Die resultierenden Ausdrücke ermöglichen es uns, die Art der Richtungsänderung der Leistung und des Energieanstiegs an der Induktivität zu erkennen, die die gleichen Schwingungen ausführt, die für die Verrichtung von Arbeit unbrauchbar sind, wie an der Kapazität.

Die in Blindlasten freigesetzte Leistung wird Blindkomponente genannt. Unter idealen Bedingungen, wenn die Anschlussdrähte keinen aktiven Widerstand aufweisen, erscheint es harmlos und verursacht keinen Schaden. Aber unter realen Leistungsbedingungen führen periodische Transienten und Blindleistungsschwankungen zu einer Erwärmung aller aktiven Elemente, einschließlich der Verbindungsdrähte, wodurch etwas Energie verbraucht wird und der Wert der angelegten vollen Leistung der Quelle abnimmt.

Der Hauptunterschied zwischen der Blindleistungskomponente besteht darin, dass sie überhaupt keine nützliche Arbeit leistet, sondern zu Verlusten an elektrischer Energie und Überlastungen der Geräte führt, die in kritischen Situationen besonders gefährlich sind.

Aus diesen Gründen ist es zur Eliminierung des Einflusses der Blindleistung, insb technische Systeme zu dessen Kompensation.

Stromverteilung bei Mischlast

Als Beispiel verwenden wir die Belastung eines Generators mit aktiver kapazitiver Charakteristik.

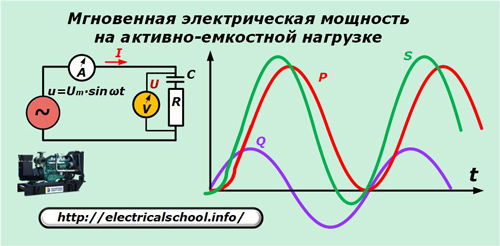
Um das Bild zu vereinfachen, sind die Sinuskurven von Strömen und Spannungen in der angegebenen Grafik nicht dargestellt. Es ist jedoch zu beachten, dass bei einer aktiv-kapazitiven Natur der Last der Stromvektor der Spannung vorauseilt.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Im ∙ sin (ωt + φ).

Nach Transformationen erhalten wir: p = P ∙ (1- cos 2ωt) + Q ∙ sin2ωt.

Diese beiden Terme im letzten Ausdruck sind die Wirk- und Blindkomponenten der momentanen Scheinleistung. Nur die erste davon leistet nützliche Arbeit.

Leistungsmessgeräte

Um den Stromverbrauch zu analysieren und zu berechnen, werden seit langem Messgeräte eingesetzt «Zähler»… Ihre Arbeit basiert darauf, die Effektivwerte von Strom und Spannung zu messen und diese automatisch mit einer Informationsausgabe zu multiplizieren.

Messgeräte zeigen den Energieverbrauch an, indem sie ab dem Einschalten des Messgeräts unter Last schrittweise die Betriebszeit von Elektrogeräten zählen.

Um den Wirkanteil der Leistung in Wechselstromkreisen zu messen, Wattmeterund reaktiv - Varmeter. Sie haben unterschiedliche Einheitenbezeichnungen:

• Watt (W, W);

• var (var, var, var).

Um den Gesamtenergieverbrauch zu ermitteln, muss sein Wert mithilfe der Leistungsdreiecksformel basierend auf den Messwerten des Wattmeters und des Varmeters berechnet werden. Es wird in einer eigenen Einheit ausgedrückt – Voltampere.

Die akzeptierten Bezeichnungen der einzelnen Einheiten helfen Elektrikern, nicht nur ihren Wert, sondern auch die Art der Leistungskomponente zu beurteilen.