Mechanische Eigenschaften eines Induktionsmotors bei verschiedenen Modi, Spannungen und Frequenzen

Die mechanischen Eigenschaften von Induktionsmotoren können als n = f (M) oder n = e(I) ausgedrückt werden. Die mechanischen Eigenschaften von Asynchronmotoren werden jedoch häufig in Form einer Abhängigkeit ausgedrückt: M = f(S), wobei C – Gleiten, S = (nc-n) / nc, wobei ns – Synchrondrehzahl ist.

In der Praxis wird für die grafische Konstruktion der mechanischen Eigenschaften eine vereinfachte Formel namens Kloss-Formel verwendet:

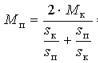
hier: Mk – kritischer (maximaler) Drehmomentwert. Dieser Momentwert entspricht dem kritischen Schlupf

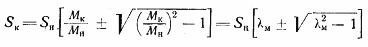
wobei λm = Mk / Mn

Die Kloss-Formel wird zur Lösung von Problemen im Zusammenhang mit dem elektrischen Antrieb mithilfe eines Induktionsmotors verwendet. Mit der Kloss-Formel können Sie ein Diagramm der mechanischen Eigenschaften gemäß den Passdaten des Induktionsmotors erstellen. Für praktische Berechnungen sollte bei der Bestimmung des kritischen Moments vor der Wurzel nur das Pluszeichen in der Formel berücksichtigt werden.

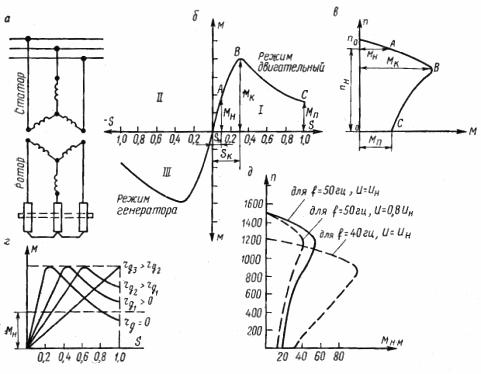
Reis. 1.Asynchronmotor: a – schematisches Diagramm, b – mechanische Eigenschaften M = f (S) – natürlich im Motor- und Generatormodus, c – natürliche mechanische Eigenschaften n = f (M) im Motormodus, d – mechanische Eigenschaften eines künstlichen Rheostaten, e – mechanische Eigenschaften für verschiedene Spannungen und Frequenzen.

Käfigläufer-Induktionsmotor

Wie aus Abb. ersichtlich ist. 1, mechanische Eigenschaften eines Induktionsmotors im I- und III-Quadranten. Der Teil der Kurve im I-Quadranten entspricht einem positiven Schlupfwert und charakterisiert den Betriebsmodus des Asynchronmotors, im III-Quadranten den Generatormodus. Von größtem praktischem Interesse ist der Motormodus.

Das Diagramm der mechanischen Eigenschaften des Motormodus enthält drei charakteristische Punkte: A, B, C und kann bedingt in zwei Abschnitte unterteilt werden: OB und BC (Abb. 1, c).

Punkt A entspricht dem Nenndrehmoment des Motors und wird durch die Formel Mn = 9,55·103·(Strn /nn) bestimmt.

Dieser Moment entspricht Nennschlupf, der für Motoren mit allgemeiner industrieller Anwendung einen Wert im Bereich von 1 bis 7 % hat, d. h. Sn = 1 — 7 %. Gleichzeitig haben kleine Motoren mehr Schlupf und große weniger.

Motoren mit hohem Schlupf, die für Stoßbelastungen vorgesehen sind, haben einen Wirkungsgrad von ca. 15 %. Hierzu zählen beispielsweise einreihige Wechselstrommotoren.

Punkt C der Kennlinie entspricht dem anfänglichen Drehmomentwert, der beim Anlauf an der Motorwelle auftritt. Dieser Moment Mp heißt initial oder beginnend. In diesem Fall ist der Schlupf gleich eins und die Geschwindigkeit ist Null. Anlaufdrehmoment Es lässt sich leicht anhand der Daten der Referenztabelle ermitteln, die das Verhältnis des Anlaufdrehmoments zum Nenn-Mp/Mn zeigt.

Die Größe des Anlaufdrehmoments bei konstanten Spannungs- und Stromfrequenzwerten hängt vom Wirkwiderstand im Rotorkreis ab. In diesem Fall steigt zunächst mit zunehmendem Wirkwiderstand der Wert des Anlaufdrehmoments und erreicht sein Maximum, wenn der Wirkwiderstand des Rotorkreises gleich dem gesamten induktiven Widerstand des Motors ist. Wenn anschließend der aktive Widerstand des Rotors zunimmt, nimmt der Wert des Anfangsdrehmoments ab und tendiert im Grenzfall gegen Null.

Punkt C (Abb. 1, b und c) entspricht einem maximalen Moment, das der Motor im gesamten Drehzahlbereich von n = 0 bis n = ns entwickeln kann. Dieses Moment wird als kritisches (oder Kipp-) Moment Mk bezeichnet . Das kritische Moment entspricht auch dem kritischen Schlupf Sk. Je kleiner der Wert des kritischen Schlupfes Sk sowie der Wert des Nennschlupfes Сn ist, desto größer ist die Steifigkeit der mechanischen Eigenschaften.

Die Start- und kritischen Momente werden durch die Nennmomente bestimmt. Laut GOST muss für elektrische Maschinen mit Käfigläufermotor die Bedingung Mn / Mn = 0,9 – 1,2, Mk / Mn = 1,65 – 2,5 erfüllt sein.

Es ist zu beachten, dass der Wert des kritischen Moments nicht vom aktiven Widerstand des Rotorkreises abhängt, während der kritische Schlupf Сk direkt proportional zu diesem Widerstand ist.Dies bedeutet, dass bei einer Erhöhung des Wirkwiderstands des Rotorkreises der Wert des kritischen Moments unverändert bleibt, sich das Maximum der Drehmomentkurve jedoch zu zunehmenden Schlupfwerten verschiebt (Abb. 1, d).

Die Größe des kritischen Drehmoments ist direkt proportional zum Quadrat der am Stator angelegten Spannung und umgekehrt proportional zum Quadrat der Frequenz der Spannungen und der Frequenz des Stroms im Stator.

Wenn beispielsweise die dem Motor zugeführte Spannung 85 % des Nennwerts beträgt, beträgt die Größe des kritischen Drehmoments 0,852 = 0,7225 = 72,25 % des kritischen Drehmoments bei Nennspannung.

Beim Ändern der Frequenz ist das Gegenteil zu beobachten. Wenn beispielsweise für einen Motor, der für den Betrieb mit einer Stromfrequenz von = 60 Hz ausgelegt ist, ein Versorgungsstrom mit einer Frequenz von = 50 Hz anliegt, liegt das kritische Moment bei (60/50)2=1,44 mal größer als der offizielle Wert seiner Häufigkeit (Abb. 1, e).

Der kritische Moment charakterisiert die momentane Überlastfähigkeit des Motors, d. h. er zeigt an, welchem ​​Überlastmoment (in wenigen Sekunden) der Motor ohne schädliche Folgen standhalten kann.

Der Abschnitt der mechanischen Kennlinie von Null bis zum maximalen (kritischen) Wert (siehe Abb. 1, biv) wird als stabiler Teil der Kennlinie bezeichnet, und der Abschnitt BC (Abb. 1, c) wird als instabiler Teil bezeichnet.

Diese Aufteilung erklärt sich aus der Tatsache, dass auf dem zunehmenden Teil der OF-Eigenschaften mit zunehmendem Schlupf, d.h. Mit abnehmender Drehzahl steigt das vom Motor entwickelte Drehmoment.Dies bedeutet, dass mit zunehmender Belastung, also mit zunehmendem Bremsmoment, die Drehzahl des Motors abnimmt und das dadurch erhöhte Drehmoment zunimmt. Bei abnehmender Belastung hingegen steigt die Drehzahl und das Drehmoment sinkt. Wenn sich die Last im gesamten Bereich des stabilen Teils der Kennlinie ändert, ändern sich Drehzahl und Drehmoment des Motors.

Der Motor kann nicht mehr als das kritische Drehmoment entwickeln, und wenn das Bremsmoment größer ist, muss der Motor zwangsläufig stoppen. Es kommt zu einem Motorüberschlag, wie man sagt.

Eine mechanische Kennlinie bei konstantem U und I und dem Fehlen eines zusätzlichen Widerstands im Rotorkreis wird als natürliche Kennlinie bezeichnet (Kennlinie eines Käfigläufermotors mit bewickeltem Rotor ohne zusätzlichen Widerstand im Rotorkreis). Als künstliche oder rheostatische Kennlinien werden solche bezeichnet, die dem zusätzlichen Widerstand im Rotorkreis entsprechen.

Alle Anlaufdrehmomentwerte sind unterschiedlich und hängen vom Wirkwiderstand des Rotorkreises ab. Unterschiedlich große Schieber entsprechen dem gleichen Nenndrehmoment Mn. Mit zunehmendem Widerstand des Rotorkreises nimmt der Schlupf zu und damit die Drehzahl des Motors ab.

Durch die Einbeziehung des aktiven Widerstands in den Rotorkreis wird die mechanische Kennlinie im stabilen Teil proportional zum Widerstand in Richtung zunehmenden Schlupfes gedehnt.Dies bedeutet, dass die Motordrehzahl abhängig von der Wellenbelastung deutlich zu variieren beginnt und die harte Charakteristik weich wird.