Dreiecke aus Spannungen, Widerständen und Leistungen
Wer sich mit Vektordiagrammen auskennt, wird leicht feststellen, dass sich auf ihnen sehr deutlich ein rechtwinkliges Spannungsdreieck erkennen lässt, dessen jede Seite Folgendes widerspiegelt: die Gesamtspannung des Stromkreises, die Spannung des aktiven Widerstands und die Spannung auf Reaktanz.
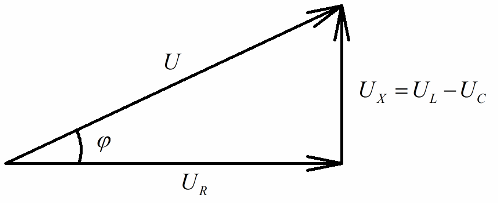
Gemäß dem Satz des Pythagoras sieht die Beziehung zwischen diesen Spannungen (zwischen der Gesamtspannung des Stromkreises und der Spannung seiner Abschnitte) wie folgt aus:
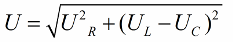
Wenn der nächste Schritt darin besteht, die Werte dieser Spannungen durch den Strom zu dividieren (der Strom fließt gleichmäßig durch alle Abschnitte der Reihenschaltung), dann durch Ohm'sches Gesetz Wir erhalten die Widerstandswerte, das heißt, wir können jetzt von einem rechtwinkligen Widerstandsdreieck sprechen:
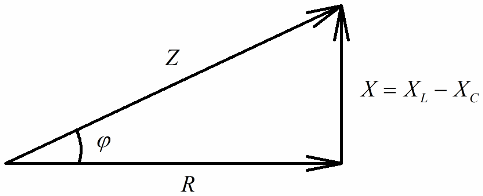
Auf ähnliche Weise (wie bei Spannungen) ist es mit dem Satz des Pythagoras möglich, einen Zusammenhang zwischen der Impedanz des Stromkreises und den Reaktanzen herzustellen. Die Beziehung wird durch die folgende Formel ausgedrückt:
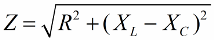
Dann multiplizieren wir die Widerstandswerte mit dem Strom, tatsächlich erhöhen wir jede Seite des rechtwinkligen Dreiecks um eine bestimmte Anzahl. Als Ergebnis erhalten wir ein rechtwinkliges Dreieck mit Kapazitäten:
Die am aktiven Widerstand des Stromkreises freigesetzte Wirkleistung, die mit der irreversiblen Umwandlung elektrischer Energie (in Wärme, bei der Ausführung von Arbeiten in der Anlage) verbunden ist, steht in klarem Zusammenhang mit der Blindleistung, die mit der reversiblen Energieumwandlung (der Erzeugung) verbunden ist von magnetischen und elektrischen Feldern in Spulen und Kondensatoren) und bei voller Stromversorgung der elektrischen Anlage.
Die Wirkleistung wird in Watt (W) gemessen, die Blindleistung in Varis (VAR – Voltampere Blindleistung) und die Gesamtleistung in VA (Voltampere).
Nach dem Satz des Pythagoras haben wir das Recht zu schreiben:
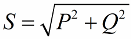
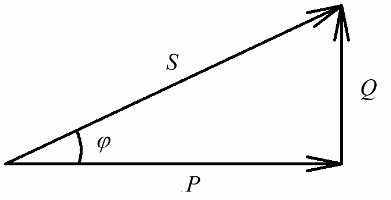
Achten wir nun darauf, dass es im Leistungsdreieck einen Winkel Phi gibt, dessen Kosinus sich vor allem durch Wirkleistung und Scheinleistung leicht bestimmen lässt. Der Kosinus dieses Winkels (cos phi) Leistungsfaktor genannt. Sie zeigt an, wie viel von der Gesamtleistung auf die Nutzarbeit in einer Elektroanlage entfällt und nicht ins Netz zurückgespeist wird.
Offensichtlich weist ein höherer Leistungsfaktor (maximal eins) auf eine höhere Umwandlungseffizienz der der Anlage zum Betrieb zugeführten Energie hin. Bei einem Leistungsfaktor von 1 wird die gesamte zugeführte Energie für die Arbeit genutzt.
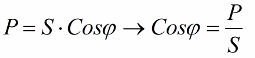
Die erhaltenen Kennzahlen ermöglichen den Ausdruck des Stromverbrauchs der Anlage in Bezug auf Leistungsfaktor, Wirkleistung und Netzspannung:
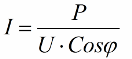
Je kleiner also der Kosinus-Phi ist, desto mehr Strom benötigt das Netzwerk, um eine bestimmte Aufgabe zu erfüllen. In der Praxis begrenzt dieser Faktor (maximaler Netzstrom) die Übertragungskapazität der Übertragungsleitung. Je niedriger der Leistungsfaktor, desto größer die Leitungslast und desto geringer die nutzbare Bandbreite (der niedrige Kosinus-Phi führt zu einer Einschränkung). Joule-Verluste in Stromleitungen mit abnehmendem Cosinus Phi können aus der folgenden Formel ermittelt werden:
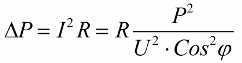
Am aktiven Widerstand R der Übertragungsleitung nehmen die Verluste umso mehr zu, je höher der Strom I ist, obwohl er reaktiv zur Last ist. Daher können wir sagen, dass bei einem niedrigen Leistungsfaktor die Kosten für die Stromübertragung einfach steigen. Dies bedeutet, dass die Erhöhung des Kosinus Phi eine wichtige volkswirtschaftliche Aufgabe ist.
Es ist wünschenswert, dass der Blindanteil der Gesamtleistung gegen Null geht. Um dies zu erreichen, wäre es sinnvoll, Elektromotoren und Transformatoren immer unter Volllast zu betreiben und sie am Ende der Nutzung abzuschalten, damit sie nicht im Leerlauf laufen. Im Leerlauf haben Motoren und Transformatoren einen sehr niedrigen Leistungsfaktor. Eine Möglichkeit, den Kosinus-Phi bei Benutzern zu erhöhen, ist die Verwendung Kondensatorbänke Und Synchronkompensatoren.
