Ein Elektron in einem elektrischen Feld

Die Bewegung eines Elektrons in einem elektrischen Feld ist einer der wichtigsten physikalischen Prozesse der Elektrotechnik. Abbildung Mal sehen, wie das im luftleeren Raum passiert. Betrachten wir zunächst ein Beispiel für die Bewegung eines Elektrons von der Kathode zur Anode in einem gleichmäßigen elektrischen Feld.

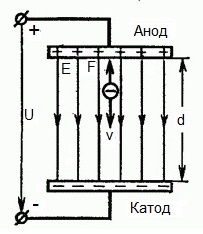
Die folgende Abbildung zeigt eine Situation, in der Elektron verlässt die negative Elektrode (Kathode) mit einer vernachlässigbar kleinen Anfangsgeschwindigkeit (die gegen Null tendiert) und tritt ein in einem gleichmäßigen elektrischen Feldzwischen zwei Elektroden vorhanden.

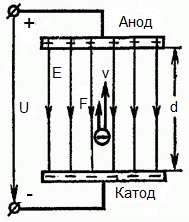
An die Elektroden wird eine konstante Spannung U angelegt und das elektrische Feld hat die entsprechende Stärke E. Der Abstand zwischen den Elektroden ist gleich d. In diesem Fall wirkt von der Seite des Feldes eine Kraft F auf das Elektron, die proportional zur Ladung des Elektrons und der Stärke des Feldes ist:

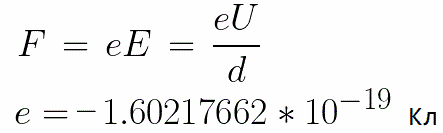
Da das Elektron negativ geladen ist, ist diese Kraft gegen den Feldstärkevektor E gerichtet. Dementsprechend wird das Elektron durch das elektrische Feld in diese Richtung beschleunigt.

Die Beschleunigung, die das Elektron erfährt, ist proportional zur Größe der auf es wirkenden Kraft F und umgekehrt proportional zur Masse m des Elektrons.Da das Feld gleichmäßig ist, kann die Beschleunigung für ein bestimmtes Bild wie folgt ausgedrückt werden:

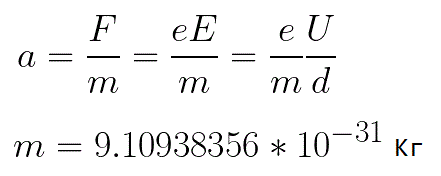
In dieser Formel ist das Verhältnis der Ladung des Elektrons zu seiner Masse die spezifische Ladung des Elektrons, eine Größe, die eine physikalische Konstante ist:

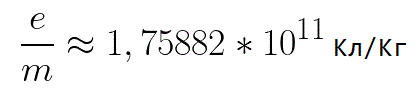
Das Elektron befindet sich also in einem beschleunigenden elektrischen Feld, da die Richtung der Anfangsgeschwindigkeit v0 mit der Richtung der Kraft F auf der Seite des Feldes zusammenfällt und sich das Elektron daher gleichmäßig bewegt. Wenn keine Hindernisse vorhanden sind, legt es den Weg d zwischen den Elektroden zurück und erreicht die Anode (positive Elektrode) mit einer bestimmten Geschwindigkeit v. In dem Moment, in dem das Elektron die Anode erreicht, ist seine kinetische Energie entsprechend gleich:

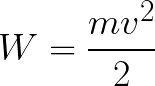
Da das Elektron auf dem gesamten Weg d durch die Kräfte des elektrischen Feldes beschleunigt wird, erhält es diese kinetische Energie durch die Arbeit der auf der Seite des Feldes wirkenden Kraft. Diese Arbeit entspricht:

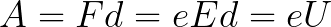
Dann kann die kinetische Energie, die das im Feld bewegte Elektron erhält, wie folgt ermittelt werden:

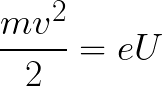
Das heißt, es ist nichts anderes als die Arbeit von Feldkräften, ein Elektron zwischen Punkten mit einer Potentialdifferenz U zu beschleunigen.

In solchen Situationen ist es zum Ausdrücken der Energie eines Elektrons zweckmäßig, eine Maßeinheit wie das „Elektronenvolt“ zu verwenden, das der Energie eines Elektrons bei einer Spannung von 1 Volt entspricht. Und da die Elektronenladung konstant ist, ist 1 Elektrovolt auch ein konstanter Wert:

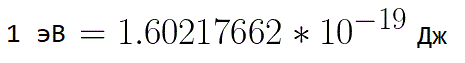
Aus der vorherigen Formel können Sie leicht die Geschwindigkeit des Elektrons an jedem Punkt seiner Bahn bestimmen, wenn es sich in einem beschleunigenden elektrischen Feld bewegt, indem Sie nur die Potentialdifferenz kennen, die es beim Beschleunigen passiert hat:

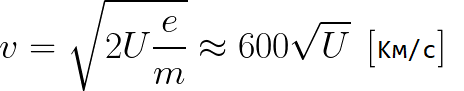
Wie wir sehen, hängt die Geschwindigkeit eines Elektrons in einem Beschleunigungsfeld nur von der Potentialdifferenz U zwischen dem Endpunkt und dem Startpunkt seiner Bahn ab.

Stellen Sie sich vor, dass sich das Elektron mit vernachlässigbarer Geschwindigkeit von der Kathode wegbewegt und die Spannung zwischen Kathode und Anode 400 Volt beträgt. In diesem Fall ist seine Geschwindigkeit im Moment des Erreichens der Anode gleich:

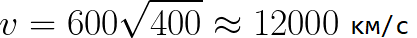
Außerdem lässt sich leicht die Zeit bestimmen, die das Elektron benötigt, um die Distanz d zwischen den Elektroden zurückzulegen. Bei einer gleichmäßig beschleunigten Bewegung aus dem Ruhezustand beträgt die Durchschnittsgeschwindigkeit die Hälfte der Endgeschwindigkeit, dann ist die Zeit des beschleunigten Fluges in einem elektrischen Feld gleich:

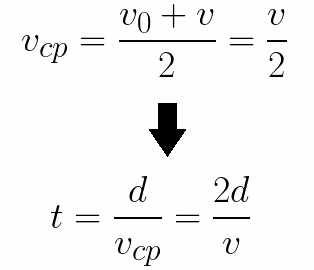
Betrachten wir nun ein Beispiel, bei dem sich ein Elektron in einem verlangsamten, gleichmäßigen elektrischen Feld bewegt. Das heißt, das Feld ist wie zuvor gerichtet, aber das Elektron beginnt, sich in die entgegengesetzte Richtung zu bewegen – von der Anode zur Kathode.

Angenommen, das Elektron verließ die Anode mit einer Anfangsgeschwindigkeit v und begann sich zunächst in Richtung der Kathode zu bewegen. In diesem Fall ist die Kraft F, die von der Seite des elektrischen Feldes auf das Elektron wirkt, gegen den elektrischen Intensitätsvektor E gerichtet – von der Kathode zur Anode.

Dadurch verringert sich die Anfangsgeschwindigkeit des Elektrons, das heißt, das Feld verlangsamt das Elektron. Das bedeutet, dass sich das Elektron unter diesen Bedingungen gleichmäßig und gleichmäßig langsam zu bewegen beginnt. Die Situation wird wie folgt beschrieben: „Ein Elektron bewegt sich in einem abbremsenden elektrischen Feld.“

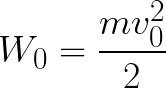
Von der Anode aus begann sich das Elektron mit einer kinetischen Energie ungleich Null zu bewegen, die während der Verzögerung abzunehmen beginnt, da die Energie nun für die Überwindung der vom Feld auf das Elektron wirkenden Kraft aufgewendet wird.

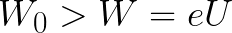
Wenn die anfängliche kinetische Energie des Elektrons beim Austritt aus der Anode sofort größer wäre als die Energie, die das Feld aufwenden muss, um das Elektron bei der Bewegung von der Kathode zur Anode zu beschleunigen (wie im ersten Beispiel), dann würde das Elektron dies tun legt eine Strecke d zurück und erreicht schließlich trotz Bremsung die Kathode.

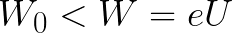
Wenn die anfängliche kinetische Energie des Elektrons unter diesem kritischen Wert liegt, erreicht das Elektron die Kathode nicht. An einem bestimmten Punkt stoppt es und beginnt dann eine gleichmäßig beschleunigte Bewegung zurück zur Anode. Dadurch gibt das Feld ihm die Energie zurück, die beim Stoppvorgang aufgewendet wurde.

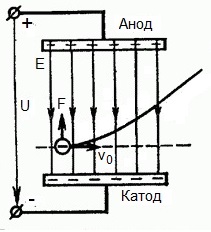
Was aber, wenn ein Elektron mit der Geschwindigkeit v0 im Wirkungsbereich eines elektrischen Feldes im rechten Winkel fliegt? Offensichtlich ist die Kraft auf der Feldseite in diesem Bereich für das Elektron von der Kathode zur Anode gerichtet, also gegen den elektrischen Feldstärkevektor E.

Das bedeutet, dass das Elektron nun zwei Bewegungskomponenten hat: die erste – mit einer Geschwindigkeit v0 senkrecht zum Feld, die zweite – gleichmäßig beschleunigt unter der Wirkung der Kraft von der zur Anode gerichteten Seite des Feldes.

Es stellt sich heraus, dass sich das Elektron, nachdem es in das Wirkungsfeld geflogen ist, auf einer parabolischen Flugbahn bewegt. Aber nachdem das Elektron den Wirkungsbereich des Feldes verlassen hat, setzt es seine gleichmäßige Bewegung aufgrund der Trägheit entlang einer geradlinigen Flugbahn fort.