Elektrokapillare Phänomene
Ist die Oberfläche des Elektrolyten geladen, so hängt die Oberflächenspannung an seiner Oberfläche nicht nur von der chemischen Zusammensetzung der benachbarten Phasen, sondern auch von deren elektrischen Eigenschaften ab. Diese Eigenschaften sind die Oberflächenladungsdichte und die Potentialdifferenz an der Grenzfläche.
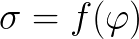
Die Abhängigkeit (e) der Oberflächenspannung von der Potentialdifferenz für dieses Phänomen wird durch eine Elektrokapillarkurve beschrieben. Und genau die Oberflächenphänomene, bei denen diese Abhängigkeit beobachtet wird, werden Elektrokapillarphänomene genannt.
Lassen Sie zu, dass sich das Elektrodenpotential an der Grenzfläche zwischen Elektrode und Elektrolyt in irgendeiner Weise ändert. In diesem Fall befinden sich auf der Metalloberfläche Ionen, die eine Oberflächenladung bilden und das Vorhandensein einer elektrischen Doppelschicht verursachen, obwohl hier überhaupt keine äußere EMF vorhanden ist.
Gleichgeladene Ionen stoßen sich über die Oberfläche der Grenzfläche gegenseitig ab und kompensieren so die Kontraktionskräfte der Flüssigkeitsmoleküle. Dadurch wird die Oberflächenspannung geringer als ohne Überpotential an der Elektrode.
Wenn an die Elektrode eine Ladung mit entgegengesetztem Vorzeichen angelegt wird, erhöht sich die Oberflächenspannung, da die Kräfte der gegenseitigen Abstoßung der Ionen abnehmen.
Bei absoluter Kompensation der Anziehungskräfte durch die elektrostatischen Kräfte der abstoßenden Ionen erreicht die Oberflächenspannung ein Maximum. Wenn wir die Ladung weiterhin zuführen, nimmt die Oberflächenspannung ab, da neue Oberflächenladungen entstehen und wachsen.
In einigen Fällen ist die Bedeutung elektrokapillarer Phänomene sehr groß. Sie ermöglichen es, die Oberflächenspannung von Flüssigkeiten und Feststoffen zu verändern sowie kolloidal-chemische Prozesse wie Adhäsion, Benetzung und Dispersion zu beeinflussen.
Wenden wir uns noch einmal der qualitativen Seite dieser Abhängigkeit zu. Thermodynamisch ist die Oberflächenspannung als die Arbeit des isothermen Prozesses zur Bildung einer einheitlichen Oberfläche definiert.
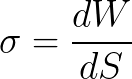
Wenn sich auf einer Oberfläche gleichnamige elektrische Ladungen befinden, stoßen sie sich gegenseitig elektrostatisch ab. Die Kräfte der elektrostatischen Abstoßung werden tangential zur Oberfläche gerichtet und versuchen, deren Fläche ohnehin zu vergrößern. Infolgedessen ist die Arbeit zum Dehnen der geladenen Oberfläche geringer als die Arbeit, die zum Dehnen einer ähnlichen, aber elektrisch neutralen Oberfläche erforderlich wäre.
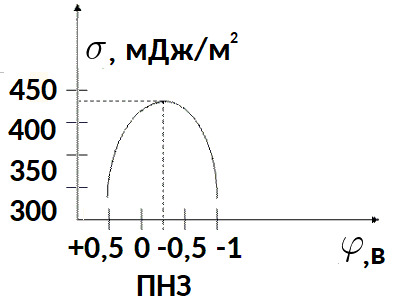
Nehmen wir als Beispiel die Elektrokapillarkurve für Quecksilber in wässrigen Elektrolytlösungen bei Raumtemperatur.
Am Punkt maximaler Oberflächenspannung ist die Ladung Null. Unter diesen Bedingungen ist die Quecksilberoberfläche elektrisch neutral.Somit ist das Potential, bei dem die Elektrodenoberflächenspannung maximal ist, das Nullladungspotential (ZCP).
Die Größe des Nullladungspotentials hängt von der Art des flüssigen Elektrolyten und der chemischen Zusammensetzung der Lösung ab. Die linke Seite der Elektrokapillarkurve, auf der das Oberflächenpotential kleiner als das Nullladungspotential ist, wird als anodischer Zweig bezeichnet. Die rechte Seite ist der Kathodenzweig.
Es ist zu beachten, dass sehr kleine Potentialänderungen (in der Größenordnung von 0,1 V) merkliche Änderungen der Oberflächenspannung (in der Größenordnung von 10 mJ pro Quadratmeter) hervorrufen können.
Die Abhängigkeit der Oberflächenspannung vom Potential wird durch die Lippmann-Gleichung beschrieben:
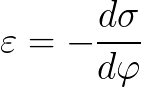
Elektrokapillarphänomene finden praktische Anwendung beim Aufbringen verschiedener Beschichtungen auf Metalle – sie ermöglichen es, die Benetzung fester Metalle mit Flüssigkeiten zu regulieren. Die Lippmann-Gleichung ermöglicht die Berechnung der Oberflächenladung und Kapazität der elektrischen Doppelschicht.
Mit Hilfe elektrokapillarer Phänomene wird die Oberflächenaktivität von Tensiden bestimmt, da ihre Ionen eine spezifische Adsorption aufweisen. In geschmolzenen Metallen (Zink, Aluminium, Cadmium, Gallium) wird deren Adsorptionskapazität bestimmt.
Die Elektrokapillartheorie erklärt die Maxima in der Polarographie. Auch die Abhängigkeit der Benetzbarkeit, Härte und des Reibungskoeffizienten der Elektrode von ihrem Potential bezieht sich auf elektrokapillare Phänomene.

